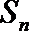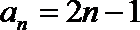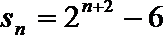- 数列
- 共2612题
17.已知等比数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
27.已知数列




(1)设

(2)设

(3)求数列

正确答案
(1)
∴
即:
∴ 
(2)
∴
又

(3)∵ 
∴
∴
解析
解析已在路上飞奔,马上就到!
知识点
17.已知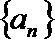
(1)求数列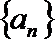
(2)若数列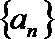
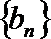

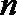

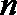
正确答案
(1)
(2)
解析
解析已在路上飞奔,马上就到!
知识点
6.已知等差数列




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知数列{an}中,an+1 =

正确答案
8
解析
解析已在路上飞奔,马上就到!
知识点
26.已知数列




(Ⅰ)求
(Ⅱ)记





正确答案
(Ⅰ)


①-②得




(Ⅱ)





解析
解析已在路上飞奔,马上就到!
知识点
3.设数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.等比数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.在等比数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 等差数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.在等差数列

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.在等比数列{an}中,首项为


(I)记


(II)若




正确答案
(I)当



当



故有


综上,A,B,C成等比数列.
(II)若

若



所以



令

因为

即得
可知满足
所以,数列


解析
解析已在路上飞奔,马上就到!
知识点
3.设n为自然数,
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析