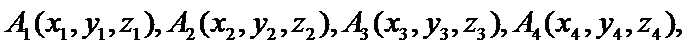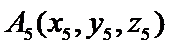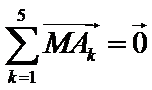- 数列
- 共2612题
17.设等差数列{an}满足a3=5,a10=-9。
（1） 求{an}的通项公式；
（2）求数列{an}的前n项和Sn及使得Sn最大的序号n的值。
正确答案
（1）由
∴
（2）由 （1）知，
∴当n = 5时，Sn取得最大
解析
解析已在路上飞奔，马上就到！
知识点
1．设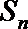
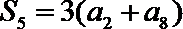
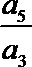
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
4．已知数列
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
14．在等比数列
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
18．数列{an}的前n项和为Sn，且Sn＝n(n＋1)(n∈N*)．
(1)求数列{an}的通项公式；
(2)若数列{bn}满足：求数列{bn}的通项公式；
(3)令cn＝(n∈N*)，求数列{cn}的前n项和Tn.
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
5．已知等比数列
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
17.设{an}是公比大于1的等比数列，Sn为数列{an}的前n项和．已知S3=7且a1+3，3a2，a3+4构成等差数列．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）令bn=lnan，n=1，2，…，求数列{bn}的前n项和Tn．
正确答案
（Ⅰ）
（Ⅱ）
解析
（I）设{an}是公比q大于1的等比数列，∵a1+3，3a2，a3+4构成等差数列，
∴6a2=a3+4+a1+3，化为6a1q=
联立解得a1=1，q=2．∴an=2n﹣1．
（II）bn=lnan=（n﹣1）ln2，∴数列{bn}的前n项和Tn=
考查方向
解题思路
（Ⅰ）由于
（Ⅱ）把第（Ⅰ）问求得
易错点
本题在第二问构造中易出现错误
知识点
4．在等差数列{
A24
B
C66
D132
正确答案
解析
由
考查方向
解题思路
根据题目条件先求出
易错点
没有记清楚等差数列的相关性质是导致本题出错的主要原因。
知识点
3．公比不为
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
14..设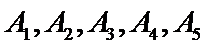
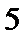
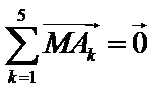
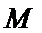
正确答案
1
解析
设
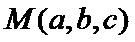
考查方向
解题思路
先设出平面向量的坐标，然后利用已知条件，求M点的坐标
易错点
设向量坐标时考虑不全
知识点
10．已知数列
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
数列
正确答案
:12
解析
由数列的前几项中可以发现每项的分子是是等差数列，分母刚好顺序相反，将上述数列分开，根据分母，1为一堆；1,2为一堆；1,2,3为一堆，1,2,3,4为一堆，依次下去求出规律，利用上述规律，求出
考查方向
本题主要考查了数列通项的定义以及对数列通项的观察能力，也是常考题型
易错点
数列规律不容易找到
知识点
17．在等比数列
正确答案
（1）
（2）由题意知：
∴
∴
解析
（1）具体的分析如下：
（2）由题意知：
∴
∴
∴
考查方向
等比数列的通项公式，裂项相消法求和．
解题思路
先求出bn，然后用裂项相消求和
易错点
分类讨论p=1和p不等1时候的情况
知识点
15．已知数列
（Ⅰ）求数列
（Ⅱ）设
正确答案
（Ⅰ）
解析
解：设等比数列
因为
所以
即
解得
所以
（Ⅱ）证明：因为
所以数列
所以
考查方向
解题思路
本题主要考查考等差、等比数列的概念和性质及方程思想，解题思路如下：1、由条件
易错点
本题第二问直接把数列
知识点
20．某农场规划将果树种在正方形的场地内．为了保护果树不被风吹，决定在果树的周围种松树．在下图里，你可以看到规划种植果树的列数（
（1）按此规律，
（2）定义：
正确答案
（1）
（2）当
解析
（1）
（2）
当
松树增加的速度快,
当
果树增加的速度快.
考查方向
本题主要考查归纳法求数列的通项公式，考查观察能力、归纳能力和即时学习能力．
解题思路
对题（1），可以通过观察、归纳得到通项公式；
对题（2），后项与前项作差比大小即可．
易错点
寻找各图中增加树木之间的关联容易出错，对新定义的概念不容易理解．
知识点
扫码查看完整答案与解析