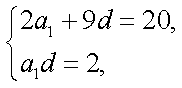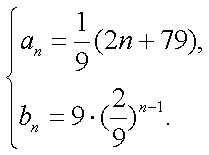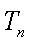- 数列
- 共2612题
4.已知一组数据4.7,4.8,5.1,5.4,5.5,则该组数据的方差是_______________.
正确答案
0.1
知识点






17.求{
18.设


正确答案
(Ⅰ)
解析
(Ⅰ)当



当






所以数列{
所以

考查方向
解题思路
(Ⅰ)先用数列第




易错点
本题在用公式法计算通项公式时n=1易丢.
正确答案
(Ⅱ)
解析
(Ⅱ)由(Ⅰ)知,

所以数列{



解题思路
(Ⅱ)根据(Ⅰ)数列{

易错点
本题在裂项中错出现错误。
设数列{





22.证明:
23.求S
正确答案
(1)由条件,对任意

因而对任意

两式相减,得

又

故对一切

解析
见答案
考查方向
解题思路
当

两式相减,得


易错点
不说明当n=1的情况导致丢分;
正确答案
解析
由(1)知,




于是

综上所述,
考查方向
解题思路
通过求数列的奇数项和偶数项的和即可得到其对应的前n项和的通项公式。
易错点
不会分类求和,或不知道该如何求和。
已知数列


22. 求q的值和
23. 设


正确答案
(I) 
解析
(I) 由已知,有

所以




当

当

所以
考查方向
解题思路
(I)由



易错点
不会讨论来解答。
正确答案
(II) 
解析
(II)解:由(I)得




上述两式相减,得

整理得,
所以,数列


考查方向
解题思路
(II)求出数列
易错点
没有掌握求和方法。



正确答案
解析
可由待定系数法求得


考查方向
解题思路
1.根据题中给出的等式找到规律;
2.根据规律得到方程组
易错点
无法发现题中给出的等式的规律导致没有思路。
知识点
设





19.求数列

20.设




正确答案
(1)

解析
(Ⅰ)设等差数列


依题意:
解得:

所以

考查方向
解题思路
问利用等差数列和等比数列的基本量求出其通项公式,
易错点
利用错位相减法求和求不对;
正确答案
解析
(Ⅱ) 


① ②得:
又
当
当

所以
考查方向
解题思路
先利用错位相减法求和,然后做差比较

易错点
不会比较

(16分)(2015•上海)已知数列{an}与{bn}满足an+1﹣an=2(bn+1﹣bn),n∈N*.
(1)若bn=3n+5,且a1=1,求数列{an}的通项公式;
(2)设{an}的第n0项是最大项,即a
(3)设a1=λ<0,bn=λn(n∈N*),求λ的取值范围,使得{an}有最大值M与最小值m,且
正确答案
1)解:∵an+1﹣an=2(bn+1﹣bn),bn=3n+5,
∴an+1﹣an=2(bn+1﹣bn)=2(3n+8﹣3n﹣5)=6,
∴{an}是等差数列,首项为a1=1,公差为6,
则an=1+(n﹣1)×6=6n﹣5;
(2)∵an=(an﹣an﹣1)+(an﹣1﹣an﹣2)+…+(a2﹣a1)+a1
=2(bn﹣bn﹣1)+2(bn﹣1﹣bn﹣2)+…+2(b2﹣b1)+a1
=2bn+a1﹣2b1,
∴
∴
∴数列{bn}的第n0项是最大项;
(3)由(2)可得
①当﹣1<λ<0时,


∴
∴λ∈
∴
②当λ=﹣1时,a2n=3,a2n﹣1=﹣1,
∴M=3,m=﹣1,

③当λ<﹣1时,当n→+∞时,a2n→+∞,无最大值;
当n→+∞时,a2n﹣1→﹣∞,无最小值.
综上所述,λ∈(﹣
知识点
(本小题满分13分)
已知等差数列



(Ⅰ)若

(ⅰ)写出数列
(ⅱ)求数列
(Ⅱ)证明:以

正确答案
考查方向
易错点
1、由题归纳法得数列
知识点
已知等差数列







正确答案
考查方向
易错点
本题易在求和项数的判断上出现错误。
知识点
已知矩阵A=


正确答案
8
解析
利用矩阵乘积运算,得出
考查方向
本题主要考查了二阶矩阵的运算
易错点
矩阵AB运算,而不是矩阵BA运算,容易概念混淆
知识点
设实数


(1)证明:当


(2)数列


正确答案
见解析。
解析
本题以二项式展开与数列变换为背景,考察学生的转化和推演能力、灵活运用能力和综合创新意识。
(1)数学归纳法证明:当p=2时,左边=(1+x)2=1+2x+x2,右边=1+2x.由于
当p=k(k>1,k为整数)时,若命题成立,则
即,p=k+1时命题也成立。
综合可见,当


(2)由

先用数学归纳法证明
①当n=1时,由题知,不等式成立;
②假设n=k(k是正整数)时不等式成立,则
由于
由于



所以,n=k+1时,不等式也成立。
综合①、②可得,对任意正整数,总有
再由

所以,
证法二:设
则其导数
因此,f(x)在定义域内是增函数。则
①当n=1时,由题知

又,
②假设n=k(k是正整数)时不等式成立,即
则

所以,n=k+1时,不等式也成立。
综合①、②可得,对任意正整数,总有
知识点
已知数列

设集合
性质1 若对于





性质2 若记





性质3 若数列




(1)若数列



(2)若数列





(3)若数列


正确答案
见解析
解析
(1)


(2)若对于








所以仅存在唯一一组


即数列








(3)若存在









下面用数学归纳法证明
显然


当


既


则










其中





所以当
即{

知识点
设








正确答案
解析
依题意得


知识点
已知各项均不为0的等差数列







17.求数列

18.设



正确答案
则

解析
则

考查方向
求数列的通项公式
解题思路
根据已知条件建立方程关系,通过求解基本量求数列通项。
易错点
注意数列类别的判定,能够根据数列的等量关系正确运算基本量
教师点评
正确列出等量关系,能够准确运算基本量是解题关键
正确答案

则
解析

则
考查方向
错位相减求和
解题思路
先根据通项写出数列,然后应用错位相减法求和
易错点
(1)在写出“Sn”与“qSn”的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“Sn-qSn”的表达式.(2)公比q为参数时要分q=1和q≠1讨论.
教师点评
注意表达式的“错项对齐”,错位后共有n+1项,∴中间n-1项是等比数列求和.
18.设等差数列
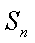
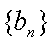

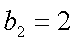
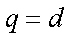
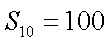
(1)求数列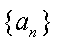
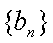
(2)当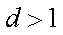
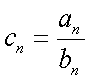
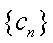
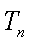
正确答案
(1)由题意有,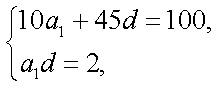
解得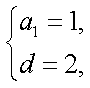
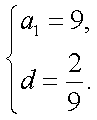
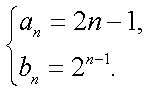
(2)由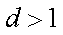
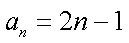
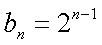
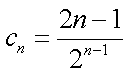
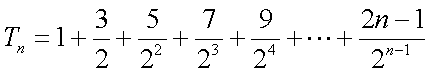
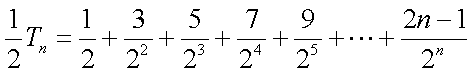
①-②可得
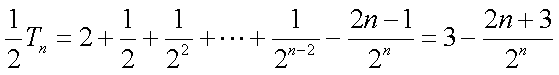
故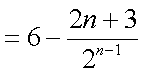
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析