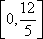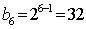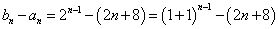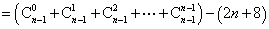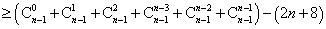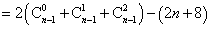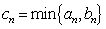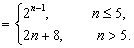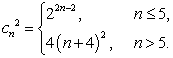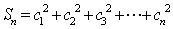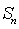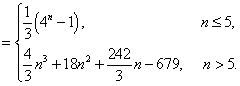- 数列
- 共2612题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
设



正确答案
解析
本题考查了等比数列的通项、前n项和公式
∵8a2+a5=0,∴q=-2,∴
知识点
设等比数列




(1)求数列
(2)在




求证:

正确答案
见解析。
解析
(1)设等比数列






即

当


即
(2)①

设

① -②得:
=
知识点
设等差数列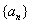
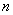
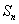
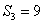
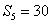

正确答案
解析
略
知识点
已知首项为
(1)求数列{an}的通项公式;
(2)设Tn=
正确答案
(1) 

解析
(1)设等比数列{an}的公比为q,
因为S3+a3,S5+a5,S4+a4成等差数列,
所以S5+a5-S3-a3=S4+a4-S5-a5,
即4a5=a3,于是
又{an}不是递减数列且

故等比数列{an}的通项公式为
(2)由(1)得
当n为奇数时,Sn随n的增大而减小,所以1<Sn≤S1=
故
当n为偶数时,Sn随n的增大而增大,所以
故
综上,对于n∈N*,总有
所以数列{Tn}最大项的值为

知识点
设a=log36,b=log510,c=log714,则( )。
正确答案
解析
根据公式变形,



知识点
设数列





(1)求
(2) 求数列
(3) 证明:对一切正整数

正确答案
见解析
解析
(1)因为



当


联立上述三个式子可得
(2)由(1)可知
当



即


所以


所以

(3) 当



当
又因为

所以
知识点
已知等比数列{an}是递增数列,Sn是{an}的前n项和,若a1,a3是方程x2-5x+4=0的两个根,则S6=__________.
正确答案
63
解析
因为x2-5x+4=0的两根为1和4,又数列{an}是递增数列,
所以a1=1,a3=4,所以q=2.
所以S6=
知识点
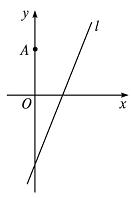
如图,在平面直角坐标系xOy中,点A(0,3),直线l:y=2x-4.设圆C的半径为1,圆心在l上。
(1)若圆心C也在直线y=x-1上,过点A作圆C的切线,求切线的方程;
(2)若圆C上存在点M,使MA=2MO,求圆心C的横坐标a的取值范围。
正确答案
(1) y=3或3x+4y-12=0 ;(2)
解析
(1)由题设,圆心C是直线y=2x-4和y=x-1的交点,解得点C(3,2),于是切线的斜率必存在。
设过A(0,3)的圆C的切线方程为y=kx+3,
由题意,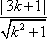
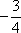
故所求切线方程为y=3或3x+4y-12=0.
(2)因为圆心在直线y=2x-4上,所以圆C的方程为(x-a)2+[y-2(a-2)]2=1.
设点M(x,y),因为MA=2MO,
所以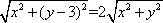
由题意,点M(x,y)在圆C上,所以圆C与圆D有公共点,则|2-1|≤CD≤2+1,
即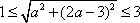
由5a2-12a+8≥0,得a∈R;
由5a2-12a≤0,得0≤a≤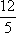
所以点C的横坐标a的取值范围为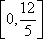
知识点
已知数列






(1)求数列
(2)若数列




正确答案
见解析。
解析
(1)解法1:当


两式相减得
即

当


∴数列


∴
解法2:由

整理得,
两边同除以

∴数列


∴
∴
当

又
∴数列

(2)解法1:∵
∴
∴

①

∴
解法2:∵
∴
∴
由
两边对

令

∴ 
知识点
已知等差数列




正确答案
20
解析
略
知识点
已知数列







(1)求数列




(3)设






正确答案
见解析。
解析
(1)




当
当


(2)由







①-②得:
(3)

又





又



设等差数列的公差为


知识点
已知等差数列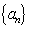
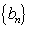
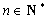
(1)求数列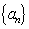
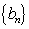
(2)设第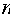
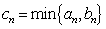
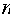
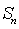
(注: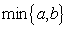

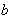
正确答案
见解析。
解析
(1)因为等差数列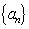
所以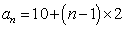
即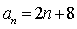
因为等比数列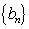
所以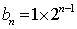
即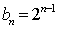
(2)因为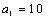
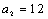
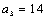
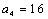
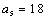
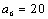
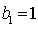
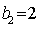
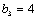
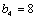
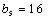
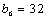
易知当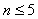
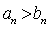
下面证明当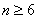
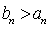
方法1:①当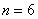
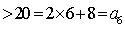
②假设当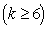
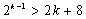
则有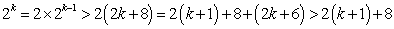
这说明当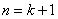
综合①②可知,不等式对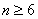
所以当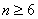
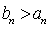
方法2:因为当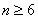
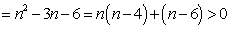
所以当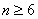

所以
则
当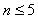
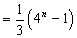
当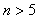
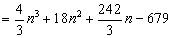
综上可知,
知识点
已知Sn是数列


(1)求
(2)求数列

(3)设数列



正确答案
见解析。
解析
(1)由


由
(2)当


①-②得

∴

∴

以上(


又
(3)∵


∴



(i)当

(ii)当
∵

∴

∴
∴
综上,当

知识点
阅读:
应用上述解法,求解下列问题:
(1)已知


(2)已知

(3)已知正数



求证:
正确答案
见解析
解析
(1)
而
当且仅当



(2)
而

当且仅当


所以函数

(3)
当且仅当

知识点
扫码查看完整答案与解析