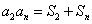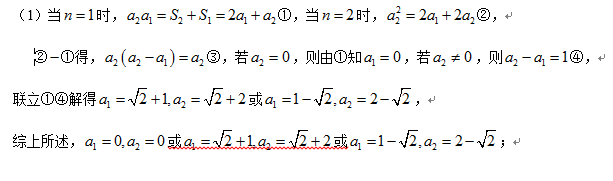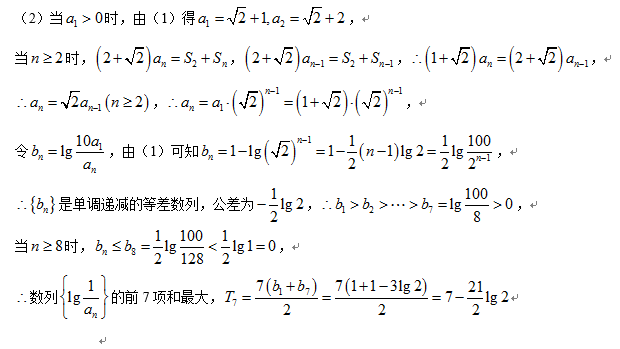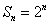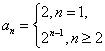- 数列
- 共2612题
设









(1)若

(2)是否存在数列
(3)是否存在数列

正确答案
见解析
解析
(1)由题意,创新数列为3,5,5,5,5的所有数列
3,5,1,2,4;……………2分
3,5,1,4,2;
3,5,2,1,4;
3,5,2,4,1;
3,5,4,1,2;
3,5,4,2,1;………………4分
(2)
知识点
已知各项为正的数列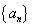
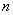
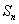
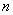
(1)求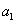
(2)求数列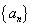
(3)若数列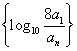
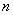
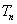
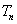
正确答案
见解析。
解析
解:
知识点
已知数列



正确答案
解析
略
知识点
已知数列



(1)求数列

(2)设


(3)设

正确答案
见解析。
解析
(1)由题意,当

两式相减得

由

所以对一切正整数n,有
故

(2)由(1),得
所以
①两边同乘以

①-②,得
所以
故
(3)由(1),得

知识点
已知数列



(1)求数列{an}的通项公式;
(2)令






正确答案
见解析。
解析
知识点
已知数列
(1)
(2)数列
正确答案
见解析。
解析
知识点
如图,三行三列的方阵有9个数
正确答案
解析
略
知识点
已知数列{an}的前n项和为Sn,a1=1,an+1=2Sn+1(n∈N*),等差数列{bn}中,b2=5,,且公差d=2.
(1)求数列{an},{bn}的通项公式;
(2)是否存在正整数n,使得a1b1+ a2b2+…+ anbn>60n?若存在,求n的最小值,若不存在,说明理由。
正确答案
见解析
解析
(1)∵an+1=2Sn+1,当n≥2时,an=2Sn-1+1两式相减得:an+1=3an(n≥2)
又a2=2a1+1=3=3a1,∴an+1=3an(n∈N*).
∴数列{an}是以1为首项,3为公比的等比数列,∴an=3n-1.
又b1=b2-d=5-2=3,∴bn= b1+(n-1)d=2n-1.………6′
(2)
令
则


①-②得:
∴Tn=n×3n>60n,即3n>60,∵33=27,34=81,∴n的最小正整数为4.………12′
知识点
已知数列



(1)设

(2)在数列
(3)若





正确答案
见解析
解析
(1)将已知条件
当


------------------3分
所以数列


-----------------4分
(2)由(1)知


-----------------1分
假设在数列






将


式得
化简得,


所以,存在满足条件的连续三项为


(3)若




得
------------------2分
由于若




① 若




② 若



③ 若




舍去;
④ 若




综上①②③④可知,只有当




时满足条件点列


------------------5分
知识点
正项数列
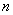

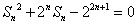
(1)求数列
(2)令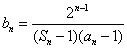
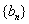
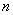
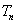
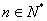
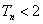
正确答案
见解析
解析
(1)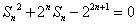
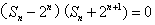
当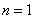
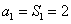
当
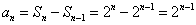
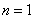
(2)当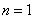
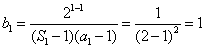
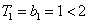
当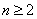
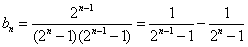
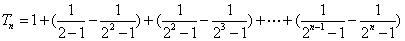
综上,对于任意的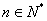
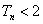
知识点
已知数列





(1)求数列

(2)设




正确答案
见解析
解析
(1)

当



所以数列

(2)


知识点
已知数列








(1)求数列
(2)若对任意的


正确答案
见解析。
解析
(1)当n=1时,
当n≥2时,
所以,





所以,
(2)由(1)得:
当n为奇数时,
因为当n为奇数时,

此时,
当n为偶数时,
因为当n为偶数时,


此时,

综上所述,对于任意的正整数n,原不等式恒成立,

知识点
若数列{an}的前n项和为 ,则下列命题:
(1)若数列{an}是递增数列,则数列{Sn}也是递增数列;
(2)数列{Sn}是递增数列的充要条件是数列{an}的各项均为正数;
(3)若{an}是等差数列(公差d

(4)若{an}是等比数列,则
其中,正确命题的个数是
正确答案
解析
数列{an}的前n项和为Sn,故 Sn =a1+a2+a3+…+an.若数列{an}是递增数列,则数列{Sn}不一定是递增数列,如当an<0 时,数列{Sn}是递减数列,故(1)不正确;由数列{Sn}是递增数列,不能推出数列{an}的各项均为正数,如数列:0,1,2,3,…,满足{Sn}是递增数列,但不满足数列{an}的各项均为正数,故(2)不正确;若{an}是等差数列(公差d≠0),则由S1•S2…Sk=0,不能推出a1•a2…ak=0,例如数列:-3,-1,1,3,满足S4=0,但 a1•a2•a3•a4≠0,故(3)不正确,若{an}是等比数列,则由S1•S2…Sk=0(k≥2,k∈N)可得数列的{an}公比为-1,故有an+an+1=0.由an+an+1=0可得数列的{an}公比为-1,可得S1•S2…Sk=0(k≥2,k∈N),故(4)正确,故选B。
知识点
已知数列





(1)求数列

(2)设




正确答案
见解析
解析
(1)

当



所以数列

(2)


知识点
已知数列



(1)求数列
(2)设




正确答案
见解析。
解析
(1)由题设知
由

所以
可见,数列

所以
(2)

=
知识点
扫码查看完整答案与解析