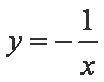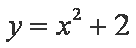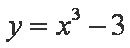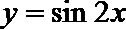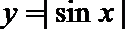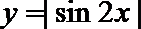函数奇偶性的判断
共53题

· 函数奇偶性的判断

函数奇偶性的判断
共53题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 14 分

已知函数，（为正常数），且函数与的图像在轴上的截距相等。

（1）求的值；

（2）若（为常数），试讨论函数的奇偶性。

正确答案

见解析

解析

（1）由题意，，即，又，故，（4分）

（2），其定义域为，（8分）

。

若为偶函数，即，则有，此时，，

故，即不为奇函数；

若为奇函数，即，则，此时，，

故，即不为偶函数；

综上，当且仅当时，函数为偶函数，且不为奇函数，（10分）

当且仅当时，函数为奇函数，且不为偶函数，（12分）

当时，函数既非奇函数又非偶函数，（14分）

知识点

函数奇偶性的判断二次函数的图象和性质

题型：简答题

简答题 · 11 分

函数，其中

（1）若是奇函数，求的值；

（2）在（1）的条件下，判别函数的图像是否存在两点A,B，使得直线AB平行于轴，说明理由；

正确答案

见解析

解析

（1）恒成立，

所以函数的定义域是R，关于原点对称（2分）

是奇函数，（3分）

（5分）

（2）假设存在两点，使得平行轴，（6分）

（7分）

，两边平方化简得到：（10分）

得到矛盾，的图像上不存在两点，使得所连的直线与轴平行（11分）

说明：证明在整个上单调递增的要4分，不证明单调性，直接说函数是单调递增的，扣3分

知识点

函数奇偶性的判断

题型：填空题

填空题 · 5 分

定义[x]表示不超过x的最大整数,例如:[1.5]=1,[-1.5]=-2,若f(x)=sin(x-[x]),则下列结论中

①f(x)是奇是函数

②f(x)是周期函数 ,周期为2π

③f(x)的最小值为0 ,无最大值

④f(x)无最小值,最大值为sin1

正确的序号为

正确答案

③

解析

则,故①错。

故②错。

是单调递增的周函数，知,

故故③正确，易知④错。综上，正确序号为③。

知识点

命题的真假判断与应用函数单调性的判断与证明函数的最值及其几何意义函数奇偶性的判断

题型：单选题

单选题 · 5 分

对于函数，下列说法正确的是

A ‍是奇函数且在（）上递增

B是奇函数且在（）上递减

C是偶函数且在（）上递增

D是偶函数且在（）上递减

正确答案

解析

略

知识点

命题的真假判断与应用函数单调性的判断与证明函数奇偶性的判断

题型：单选题

单选题 · 5 分

下列函数中，与函数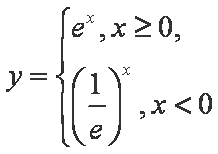的奇偶性相同，且在上单调性也相同的是( )

正确答案

解析

略

知识点

函数单调性的判断与证明函数奇偶性的判断

题型：单选题

单选题 · 4 分

17．在下列函数中，既是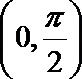上的增函数，又是以为最小正周期的偶函数的函数是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数单调性的判断与证明函数奇偶性的判断函数的周期性

题型：单选题

单选题 · 5 分

2.函数的奇偶性是（）

A是奇函数

B是偶函数

C是非奇非偶函数

D以上都不对

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数奇偶性的判断

题型：填空题

填空题 · 4 分

11．已知函数满足如下性质：

①函数的定义域为；

②为上的奇函数；

③的值域为；

④在上为增函数，

写出满足上述性质的一个函数为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的定义域及其求法函数的值域函数单调性的判断与证明函数奇偶性的判断

题型：单选题

单选题 · 5 分

7．已知函数则下列正确的是（）

A是偶函数，有最大值为

B是偶函数，有最小值为

C是偶函数，有最大值为2

D是奇函数，没有最小值

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数奇偶性的判断二次函数在闭区间上的最值三角函数的最值

题型：简答题

简答题 · 14 分

19．已知：函数的定义域为，且满足对于任意，都有。

（1）求：的值；　　

（2）判断的奇偶性并证明；

（3）如果，，且在上是增函数，求：的取值范围。

正确答案

（1）解：令，则，

（2）证明：令，则，
　　　　　　　令，，则，即，∴为偶函数，

（3）∵，，

∴即为（1）

∵上是增函数，

∴（1）等价于不等式组：或，

则或，

∴

解析

解析已在路上飞奔，马上就到！

知识点

函数单调性的性质函数奇偶性的判断抽象函数及其应用函数的值

继续学习学习下一知识点

下一知识点 : 函数奇偶性的性质

百度题库 > 高考 > 理科数学 > 函数奇偶性的判断

扫码查看完整答案与解析