函数奇偶性的判断
共53题

· 函数奇偶性的判断

函数奇偶性的判断
共53题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 5 分

15．已知集合M是满足下列条件的函数f(x)的全体：

（1）f(x)既不是奇函数也不是偶函数；

（2）函数f(x)有零点．

那么在函数

①f(x)＝|x|－1，

②f(x)＝2x－1，

③f(x)＝，

④f(x)＝x2－x－1＋ln x

中属于M的有．(写出所有符合的函数序号)

正确答案

②④

解析

解析已在路上飞奔，马上就到！

知识点

函数奇偶性的判断函数零点的判断和求解

题型：单选题

单选题 · 5 分

5．若函数，则下列结论正确的是（）

A，在上是增函数

B，在上是减函数

C，是偶函数

D，是奇函数

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数奇偶性的判断

题型：单选题

单选题 · 5 分

12．有以下四个命题：

① 是奇函数充要条件是；

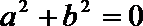
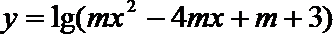
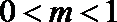
② 若的定义域为R，则；

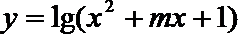
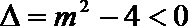
③ 若的值域为R，则；

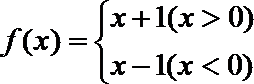
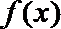
④ 若，则是奇函数；

则以上正确命题个数有（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

命题的真假判断与应用函数奇偶性的判断对数函数的定义域对数函数的值域与最值

题型：简答题

简答题 · 18 分

20．函数的定义域，对定义域内任意两个实数，都有成立．

（1）求的值并证明为偶函数；

（2）若，记，求数列的前2009项的和；

（3）若，且不等式对任意正实数恒成立，求非零实数a的取值范围．

正确答案

（1）赋值得，

为偶函数

（2）得，

；

，

（3）设，

，

得

恒成立，

又，

从而

解析

解析已在路上飞奔，马上就到！

知识点

函数奇偶性的判断抽象函数及其应用函数的值由递推关系式求数列的通项公式数列与不等式的综合

题型：简答题

简答题 · 14 分

20．设6张卡片上分别写有函数、、、、和．

（1）现从盒子中任取两张卡片，将卡片上的函数相加得一个新函数，求所得函数是奇函数的概率；

（2）现从盒子中进行逐一抽取卡片，且每次取出后均不放回，若取到一张记有偶函数的卡片，则停止抽取，否则继续进行，求抽取次数的分布列和数学期望．

正确答案

解：（1）记事件A为“任取两张卡片，将卡片上的函数相加得到的函数是奇函数”，则

（2）可取1，2，3，4．，，

，

故ξ的分布列为

，从而的数学期望为．

解析

解析已在路上飞奔，马上就到！

知识点

函数奇偶性的判断古典概型的概率离散型随机变量及其分布列、均值与方差

题型：单选题

单选题 · 5 分

3．下列函数中，既是偶函数，又是在区间上单调递减的函数是（）

正确答案

解析

非奇非偶函数，排除B,当时，函数单调递增，排除C, 在定义域上不单调，排除D,选A．

知识点

函数单调性的判断与证明函数奇偶性的判断

题型：单选题

单选题 · 5 分

6.对函数现有下列命题:

①函数是偶函数;

②函数的最小正周期是

③点是函数的图像的一个对称中心;

④函数在区间上单调递增,在区间上单调递减.

其中是真命题的是( )

A①③

B①④

C②③

D②④

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

命题的真假判断与应用函数的单调性及单调区间函数奇偶性的判断奇偶函数图象的对称性函数的周期性

题型：简答题

简答题 · 14 分

19．已知函数．

（1）求函数的定义域，并求的值

（2）若，当时, 是否存在最小值, 若存在, 求出最小值; 若不存在, 请说明理由。

正确答案

解：（1）由得，

∴函数的定义域是

∵，

∴是奇函数

∴＝0

（若直接代入计算也给分）

（2） ∵对恒成立

∴在上是减函数

∴

解析

解析已在路上飞奔，马上就到！

知识点

函数的定义域及其求法函数单调性的性质函数奇偶性的判断函数的值

题型：简答题

简答题 · 16 分

20.已知函数。

（1）若函数是其定义域上的增函数，求实数的取值范围；

（2）若是奇函数，且的极大值是，求函数在区间上的最大值；

（3）证明：当时，。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数奇偶性的判断

题型：单选题

单选题 · 5 分

2.下列函数为偶函数的是（）

D[来

正确答案

解析

A选项的定义域是，关于原点对称，因为，所以是奇函数；B选项的定义域是，关于原点对称，因为，，所以是非奇非偶函数；C选项的定义域是，关于原点对称，因为，所以是偶函数；D选项的定义域是，关于原点对称，因为，所以是奇函数．故选C．

知识点

偶函数函数奇偶性的判断

继续学习学习下一知识点

下一知识点 : 函数奇偶性的性质

百度题库 > 高考 > 理科数学 > 函数奇偶性的判断

扫码查看完整答案与解析