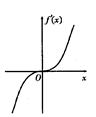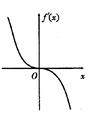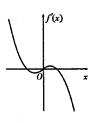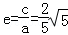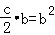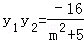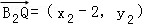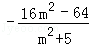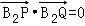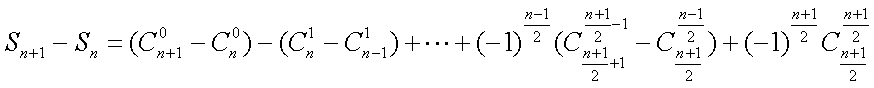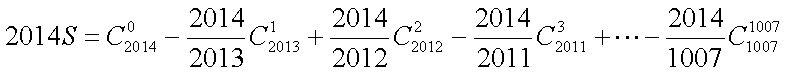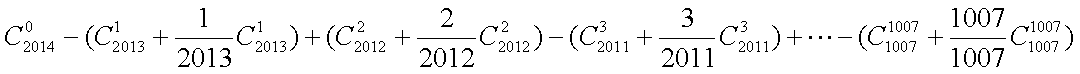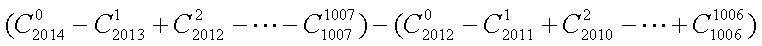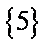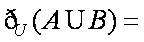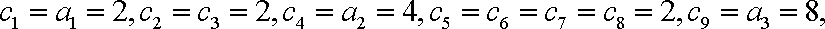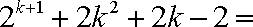- 幂函数的图像
- 共352题
已知在平面直角坐标系中有一个点列:






正确答案
解析
略
知识点
已知函数 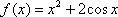
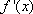
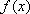
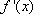
正确答案
解析
略
知识点
函数
正确答案
解析
略
知识点
(1)1证明两角和的余弦公式
2由

(2)已知△ABC的面积

正确答案
见解析。
解析
知识点
某射手射击所得环数
已知

正确答案
0.4
解析
由表格可知:
联合解得
知识点


正确答案
20
解析
略
知识点
设函数f(x),g(x)的定义域都为R,且f(x)是奇函数,g(x)是偶函数,则下列结论中正确的是( )
正确答案
解析
由于偶函数的绝对值还是偶函数,一个奇函数与一个偶函数之积为奇函数,故正确选项为C.
知识点
如图,设椭圆的中心为原点O,长轴在x轴上,上顶点为A,左右焦点分别为F1,F2,线段OF1,OF2的中点分别为B1,B2,且△AB1B2是面积为4的直角三角形。
(1)求该椭圆的离心率和标准方程;
(2)过B1做直线l交椭圆于P,Q两点,使PB2⊥QB2,求直线l的方程。
正确答案
见解析
解析
(1)设椭圆的方程为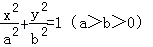
∵ △AB1B2是的直角三角形,|AB1|=AB2|,∴ ∠B1AB2为直角,从而|OA|=|OB2|,即
∵ c2=a2﹣b2,∴ a2=5b2,c2=4b2,∴
在△AB1B2中,OA⊥B1B2,∴ S=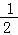
∵ S=4,∴b2=4,∴ a2=5b2=20
∴ 椭圆标准方程为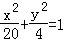
(2)由(1)知B1(﹣2,0),B2(2,0),由题意,直线PQ的倾斜角不为0,故可设直线PQ的方程为x=my﹣2
代入椭圆方程,消元可得(m2+5)y2﹣4my﹣16﹣0①
设P(x1,y1),Q(x2,y2),
∴ 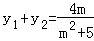
∵ 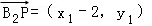
∴ 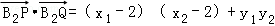
∵ PB2⊥QB2,∴
∴ 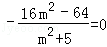
所以满足条件的直线有两条,其方程分别为x+2y+2=0和x﹣2y+2=0。
知识点
下列四个函数中,在(0,1)上为增函数的是
正确答案
解析
略
知识点
已知函数
正确答案

解析
略
知识点
设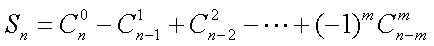
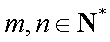
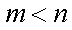
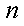
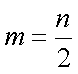
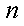
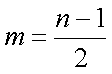
(1)证明:当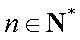

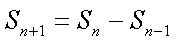
(2)记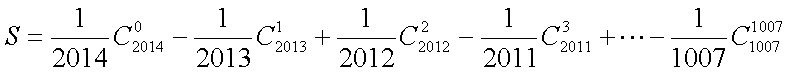
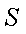
正确答案
见解析。
解析
(1)当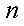
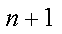
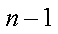
∵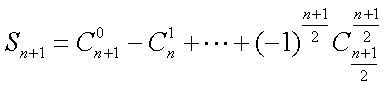
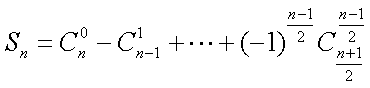
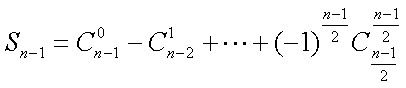
∴
=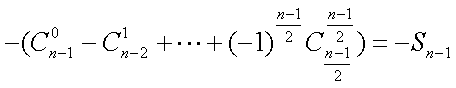
∴当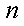
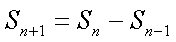
同理可证,当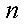
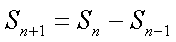
(2)由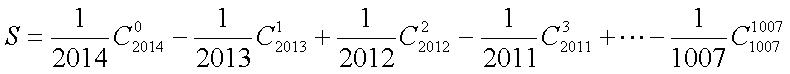
=
=
=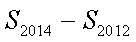
又由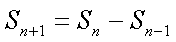
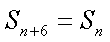
所以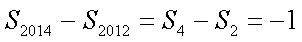
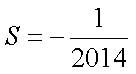
知识点
已知集合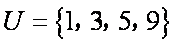
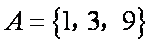
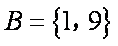
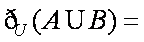
正确答案
解析
易得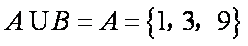
知识点
假设在5秒内的任何时刻,两条不相关的短信机会均等地进人同一部手机,若这两条短信进人手机的时间之差小于2秒,手机就会受到干扰,则手机受到干扰的概率为
正确答案
解析
设两条短信分别在时刻x、y进人手机,则0<x<5,0<y<5,“手机受到干扰”就是“|x-y|<2”在直角坐标系中,作出点P(x,y)所在区域(如右图).由几何概型知,手机受到干扰的概率为
知识点
设函数
(1)当

(2)证明:对

(3)若


正确答案
见解析
解析
(1)


则


当



当



所以 


(2)因为 

所以当




(3)(证法一)数学归纳法
ⅰ)当
ⅱ)假设当
即若

当





设
由(2)得
=
=
由假设可得 
所以当 
由ⅰ),ⅱ)可知,对一切正整数n∈N*,命题都成立,
所以 若


(证法二)若
那么由(2)可得

知识点
已知矩阵







正确答案
见解析。
解析
由题意知,

所以

所以

知识点
设函数
(1)求函数
(2)设




(3)若



正确答案
见解析
解析
解析:(1)因为

解得:



由


所以

因为
所以函数

(2)由(1)知,当

“对任意








因为
① 当


② 当




所以
③ 当









令







所以
综上所述,若对任意


则实数

(3)证明:由(1)知,当


当






所以
又因为
所以



当且仅当
知识点
如果存在常数







(1)若数列:



(2)已知有穷等差数列





(3)对于一个不少于3项,且各项皆为正整数的递增数列
正确答案
见解析
解析
(1)因为数列:

所以

故
即
(2)设数列



若
即对数列

同理可得:若

由“兑换数列”的定义可知,数列

又因为数列



(3)假设存在这样的等比数列

因为数列
则
又因为数列


故数列

则
①若




②若

即


综合①②得,不存在满足条件的数列
知识点
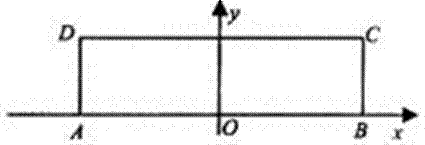
已知长方形ABCD,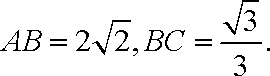

(1)求以A,B为焦点,且过C,D两点的椭圆P的标准方程;
(2)已知定点E(—1,0),直线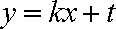

正确答案
见解析。
解析
(1)由题意可得点A,B,C的坐标分别为
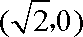
设椭圆的标准方程是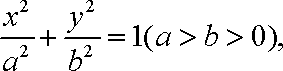
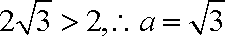
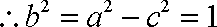
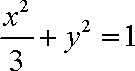
(2)将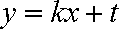
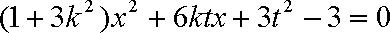
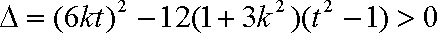
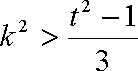
设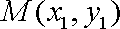
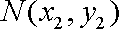
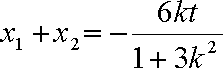
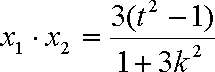
因为以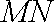

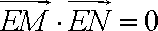
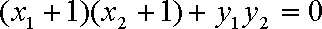
而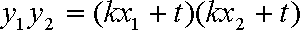
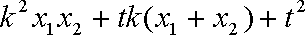
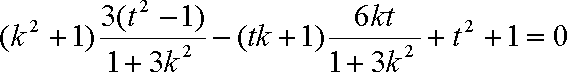
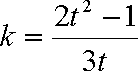
如果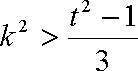

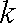
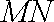

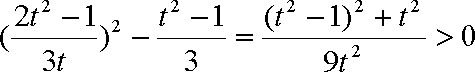
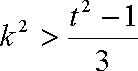

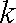
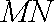

知识点
已知矩阵


正确答案
见解析。
解析
矩阵M的特征多项式为
令


令

知识点
已知数列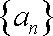
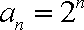
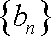
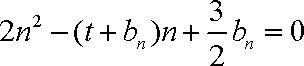
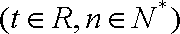
(1)试确定实数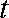
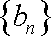
(2)当数列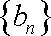
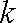
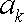
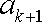
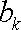
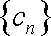
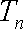

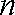
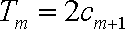
正确答案
见解析
解析
(1)当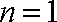
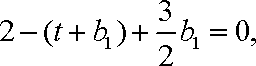
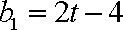
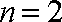
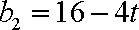

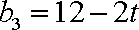
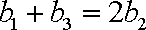
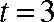
而当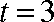
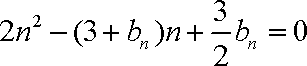
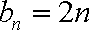
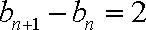
故此时数列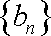
(2)由题意知,
则当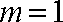
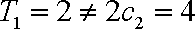
当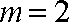
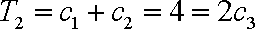
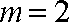
当
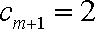
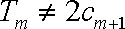
从而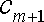
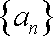
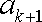

b1个 b2个 b3个 bk个
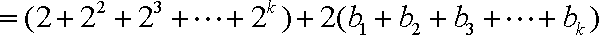
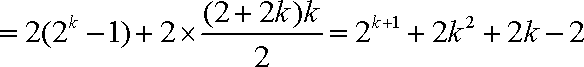
又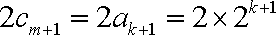
所以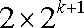
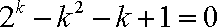
所以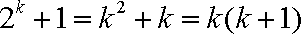
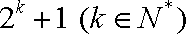
而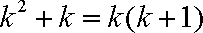
即当
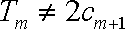
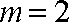
知识点
扫码查看完整答案与解析