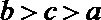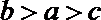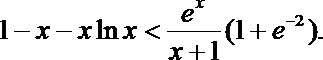- 幂函数的图像
- 共352题
20.在





(Ⅰ)求


(Ⅱ)求
正确答案
(Ⅰ)


由余弦定理可得:






(Ⅱ)在






解析
解析已在路上飞奔,马上就到!
知识点
5. 如果若干个函数的图象经过平移后能够重合,则称这些函数为“同簇函数”.给出下列函数:
①
②
③ 
④ 
其中“同簇函数”的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6. 一个几何体的正视图、侧视图、俯视图如图所示,则该几何体的表面积和体积分别为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12. 可导函数
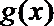

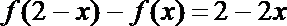
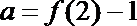



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14. 若函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22. 已知函数


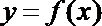


(1)求
(2)求
(3)设
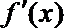



正确答案
(1)由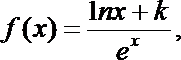
由于曲线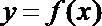

所以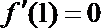
(2)由(1)得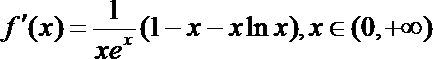
令


当


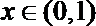
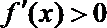
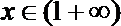

因此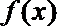
(3)证明:因为
所以
因此对任意
由(2)知
所以
因此当



所以


因为


故


因此对任意
解析
解析已在路上飞奔,马上就到!
知识点
5.若对任意正实数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.一无穷等比数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.某加油站拟造如图所示的铁皮储油罐(不计厚度,长度单位:米),其中储油罐的中间为圆柱形,左右两端均为半球形,





(1)写出

(2)求该储油罐的建造费用最小时的
正确答案
(1)


(2)

所以当
解析
解析已在路上飞奔,马上就到!
知识点
19.解关于
正确答案









解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析