- 幂函数的图像
- 共352题
函数














正确答案
解析
因为函数



即

















知识点
设函数
(1)若函数
(2)当a>0时,求
正确答案
见解析。
解析
(1)
①
②当
即
(2)①当
②当
知识点
已知函数f(x)=lnx﹣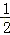
(1)试用含有a的式子表示b,并求f(x)的单调区间;
(2)设函数f(x)的最大值为g(a),试证明不等式:g(a)>ln(1+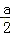
(3)首先阅读材料:对于函数图象上的任意两点A(x1,y1),B(x2,y2)(x1<x2),如果在函数图象上存在点M(x0,y0)(x0∈(x1,x2)),使得f(x)在点M处的切线l∥AB,则称AB存在“相依切线”特别地,当x0=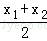
正确答案
见解析
解析
(1)f(x)的定义域为(0,+∞),
∵f′(x)=
∴b=a﹣1,∴f′(x)=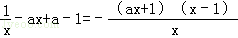
当f′(x)>0时,得﹣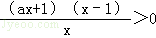
∵x>0,a>0,解得0<x<1,
当f′(x)<0时,得﹣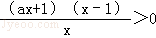
∴当f(x)在(0,1)上单调递增,在(1,+∞)上单调递减;
(2)证明:g(a)=f(1)=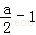
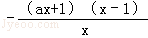
令φ(a)=ln(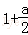
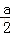

∴φ(a)在(0,+∞)上是减函数,
∴φ(a)<φ(0)=0,即ln(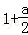
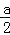
(3)假设函数f(x)的图象上存在两点A(x1,y1),B(x2,y2),使得AB存在“中值相依切线”,
则kAB=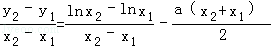
f′(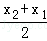
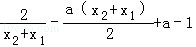
又kAB=f′(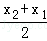
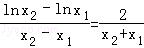
∴ln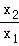
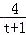
令h(t)=lnt+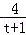
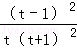
∴h(t)是(1,+∞)上的增函数,
∴h(t)>h(1)=0,与lnt=2﹣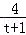
∴函数f(x)的图象上不存在两点A(x1,y1),B(x2,y2),使得AB存在“中值相依切线”。
知识点
复数

正确答案
解析


知识点
已知直线






正确答案
2
解析
因为







知识点
扫码查看完整答案与解析







