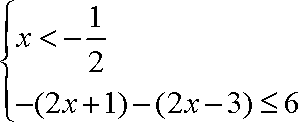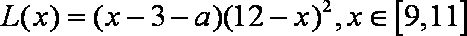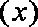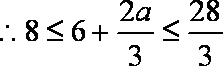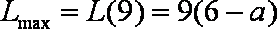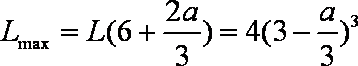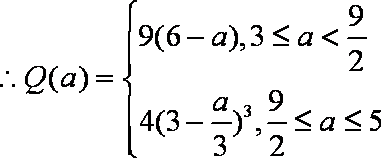- 幂函数的图像
- 共352题
在



(1)若
(2)求
正确答案
见解析
解析
由已知及正弦定理得
即

故

(1)由

所以△
(2)
又


知识点
设函数

(1)求
(2)若






正确答案
(1)
当


当

(2)AC=3,BC=
解析
(1)




当


当


(2)因为
即
∴
∵


∴

由余弦定理得:
∴
知识点
已知函数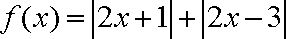
(1)求不等式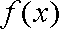
(2)若关于x的不等式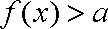
正确答案
(1)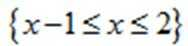
解析
(1)原不等式等价于
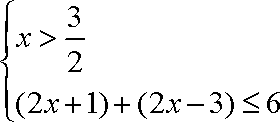
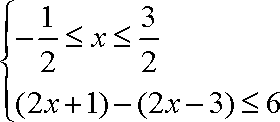
解得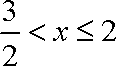
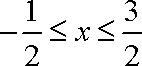
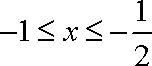
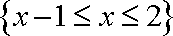
(2)∵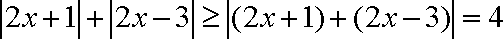
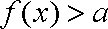
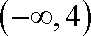
知识点
设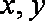
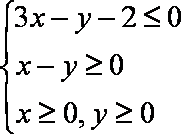
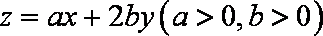
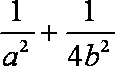
正确答案
8
解析
略
知识点
将函数f(x)=2sin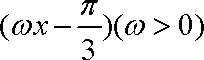
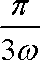
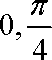
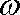
正确答案
解析
将函数f(x)=2sin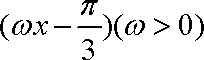
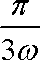
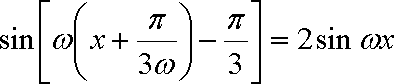
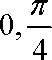
∴ 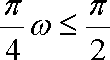
知识点
已知函数y=f(x)的周期为2,当x∈[0,2]时,f(x)=(x﹣1)2,如果g(x)=f(x)﹣log5|x﹣1|,则函数y=g(x)的所有零点的个数是( )
正确答案
解析
由题意可得g(x)=f(x)﹣log5|x﹣1|,根据周期性画出函数f(x)=(x﹣1)2的图象以及y=log5|x﹣1|的图象
根据y=log5|x﹣1|在(1,+∞)上单调递增函数,当x=6 时,log5|x﹣1|=1,
∴ 当x>6时,y=log5|x﹣1|>1,此时与函数y=f(x)无交点。
再根据y=log5|x﹣1|的图象和 f(x)的图象都关于直线x=1对称,结合图象可知有8个交点,则函数g(x)=f(x)﹣log5|x﹣1|的零点个数为 8,
故选D
知识点
已知函数
(1)当a=1时,求
(2)对任意的
正确答案
(1)单调减区间为(0,2],单调增区间为(2,+
(2)
解析
(1)当a=1时,f(x)=x-1-2lnx,则

由

故函数f(x)的单调减区间为(0,2],单调增区间为(2,+
(2)对任意的


令l(x)=


再令m(x)=


故m(x)在

从而

所以,l(x)<l(


知识点
产品每件产品成本3元,且每件产品需向总公司交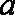
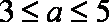
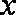
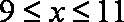
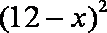
(1)求分公司一年的利润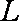
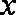
(2)当每件产品的售价为多少元时,分公司一年的利润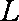
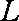
正确答案
(1)
(2)若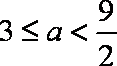
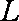
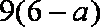
若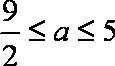
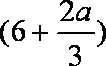
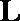
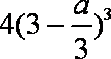
解析
(1)
(2)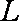
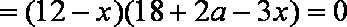
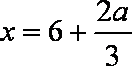
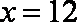
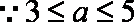
①当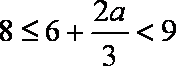
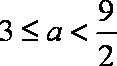
②当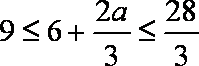
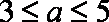
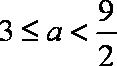
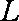
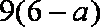
若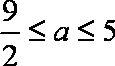
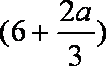
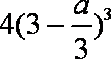
知识点
在极坐标系呶中,Ox为极点,点A(2,

(1)求经过O,A,B的圆C的极坐标方程;
(2)以极点为坐标原点,极轴为x轴的正半轴建立平面直角坐标系,圆D的参数方程为
正确答案
见解析
解析
(1)
(2))

知识点
已知函数f(x)=ax+lnx,其中a为常数,设e为自然对数的底数.
(1) 当a=-1时,求f(x)的最大值;
(2) 若f(x)在区间(0,e]上的最大值为-3,求a的值;
(3) 当a=-1时,试推断方程

正确答案
(1)-1(2)
解析
(1) 当a=-1时,f(x)=-x+lnx,f′(x)=-1+
当0<x<1时,f′(x)>0;当x>1时,f′(x)<0.
∴f(x)在(0,1)上是增函数,在(1,+∞)上是减函数…………3分

(2) ∵f′(x)=a+


① 若a≥
∴
② 若a<

由f(x)<0

从而f(x)在

∴


令-1+ln

∴





(3) 由(Ⅰ)知当a=-1时
∴|f(x)|≥1……………………………………………………………10分
又令g(x)=

当0<x<e时,g′(x)>0,g(x) 在(0,e)单调递增;
当x>e时,g′(x)<0,g(x) 在(e,+∞)单调递减…………………………11分
∴

∴|f(x)|>g(x),即|f(x)|> 
∴方程|f(x)|=
知识点
扫码查看完整答案与解析