- 余弦定理
- 共145题
16.





(1)求

(2)在△ABC中,




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.在△ABC中,角A,B,C的对边分别为a,b,c,且
(1)求角
(2)若角




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.在





(1)若


(2)求
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.在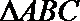
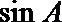
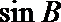
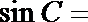
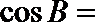
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知函数
(Ⅰ)求函数
(Ⅱ)设






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16. 已知向量

(1) 求角C的大小;
(2) 求
正确答案
(1)由

即
由余弦定理得
∵
∴
(2) ∵
∴
∵ 
∴
∴
解析
解析已在路上飞奔,马上就到!
知识点
19.如图,在△ABC中,

(1)求BC的长;
(2)求△DBC的面积。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15. 已知在



正确答案
解析
因为



考查方向
解题思路
由正弦定理整理,二倍角正弦公式
易错点
正弦定理的转化
知识点
17.



(Ⅰ)求角
(Ⅱ)若

正确答案
(Ⅰ)
(Ⅱ)
解析
试题分析:本题属于解三角形中的基本问题,难度不大。此类问题主要应用正(余)弦定理进行恒等变换;注意边和角的统一。
(Ⅰ)在

所以
因为
所以

解得
因为

(Ⅱ)由正弦定理,
所以

因为

所以


考查方向
解题思路
本题主要考查正(余)弦定理、和(差)角公式和三角函数的恒等变换等知识,
解题步骤如下:
利用降幂公式和三角变换化成关于cosC的一元二次方程;
利用正弦定理把边化成角,从而求出
易错点
第一问中降幂公式往往会出错;
第二问中角A的范围和
知识点
16.在△ABC中,角A、B、C的对边分别为a、16.在△ABC中,角A、B、C的对边分别为a、b、c,若2ccosB=2a+b,△ABC的面积为S=
正确答案
解析
在
即
再由余弦定理可得,
整理可得
即
考查方向
解题思路
本题主要考查了正余弦定理在解三角形中的应用及诱导公式和两角和的正弦公式、基本不

易错点
本题在化边为角的过程中易错
知识点
扫码查看完整答案与解析