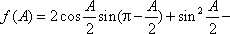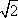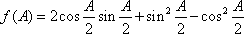- 余弦定理
- 共145题
1
题型:简答题
|
在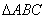
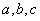
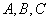
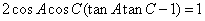
(1)求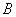
(2)若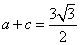
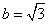
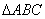
正确答案
见解析
解析
知识点
三角函数中的恒等变换应用正弦定理余弦定理
1
题型:简答题
|
在



(1)求
(2)若


正确答案
见解析
解析
(1)由




(2)由余弦定理得:

又



知识点
三角函数中的恒等变换应用正弦定理余弦定理
1
题型:简答题
|
在




(1)求角
(2)若



正确答案
(1)
解析
(1)因为
所以
因为

所以
因为


(2)因为

所以由余弦定理得

解得

所以


知识点
正弦定理余弦定理
1
题型:简答题
|
已知△ABC中,∠A, ∠B, ∠C的对边长分别为


(1)求c的值;
(2)求
正确答案
(1)
(2)
解析
知识点
正弦定理余弦定理利用基本不等式求最值
1
题型:简答题
|
在△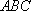
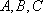
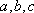
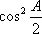
(1)求函数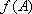
(2)若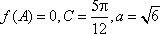
正确答案
(1)
(2)3
解析
(1)因为

因为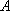
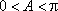
所以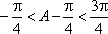
所以当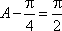
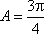
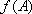
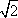
(2)由题意知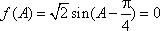
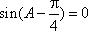
又因为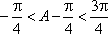
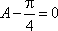

又因为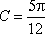
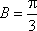
由正弦定理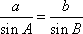
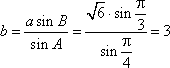
知识点
三角函数中的恒等变换应用正弦定理余弦定理
下一知识点 : 余弦定理的应用
扫码查看完整答案与解析