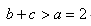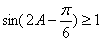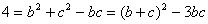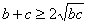- 余弦定理
- 共145题
1
题型:填空题
|
在




正确答案
3
解析
略
知识点
同角三角函数间的基本关系余弦定理
1
题型:简答题
|
在△ABC中,已知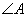

(1)将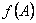
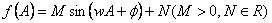
(2)若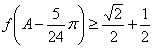
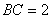
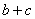
正确答案
(1)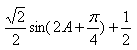
解析
(1)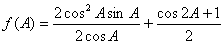
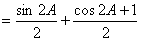
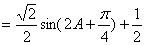
(2) 由条件及(1)得: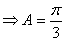
由余弦定理得:
由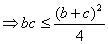
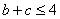
又
因此,
知识点
两角和与差的正弦函数二倍角的余弦余弦定理三角函数的最值
1
题型:简答题
|
如图,已知平面上直线














(1) 判断三角形
(2)记

正确答案
见解析。
解析
(1)由正弦定理得:








(2)





知识点
余弦定理
1
题型:简答题
|
在



(1)求角
(2)若





正确答案
(1)
解析
(1)∵
∴
又
∴
(2)∵
∴
同理
∴
∵

∴


知识点
正弦定理余弦定理三角函数的最值
1
题型:填空题
|
在




正确答案
解析
略
知识点
同角三角函数基本关系的运用余弦定理
下一知识点 : 余弦定理的应用
扫码查看完整答案与解析