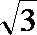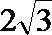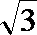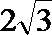余弦定理
共145题

· 余弦定理

余弦定理
共145题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 20 分

开学初，小源到建设银行营业网点兑换了此前在网上预约的中国高铁纪念币。这枚纪念币由中国人民银行发行，面额10元，每人限兑20枚，且需要提前预约。小源打算与班上同学分享自己的喜悦。他可以向大家这样介绍

①纪念币面额和实际购买力都是由中国人民银行规定的

②纪念币可以直接购买商品，也具有支付手段等货币职能

③纪念币发行量有限，具有一定的收藏价值和升值空间

④纪念币不能与同面额人民币等值流通，必须在规定时间地点使用

A①③

B①④

C②③

D②④

正确答案

解析

①错误，国家无权规定纪念币的实际购买力；④错误，纪念币与同面额人民币等值流通，在任何时间地点都可使用；由中国人民银行发行的纪念币属于法定货币，可以直接购买商品，也具有支付手段等货币职能，因其发行量有限，具有一定的收藏价值和升值空间，故②③正确。

知识点

生产决定消费

题型：简答题

简答题 · 12 分

19．如图，海上有两个小岛相距10，船O将保持观望A岛和B岛所成的视角为，现从船O上派下一只小艇沿方向驶至处进行作业，且．设。

（1）用分别表示和，并求出的取值范围；

（2）晚上小艇在处发出一道强烈的光线照射A岛，B岛至光线的距离为，求BD的最大值．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数单调性的判断与证明余弦定理解三角形的实际应用利用基本不等式求最值

题型：简答题

简答题 · 14 分

22．在△ABC中，AB＝3，AC边上的中线BD＝，＝5

（1）求AC的长；

（2）求sin（2A－B）的值.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

正弦定理余弦定理平面向量数量积的运算

题型：简答题

简答题 · 12 分

16．已知向量，函数的最小正周期为．

（I）求函数的单调增区间；

（II）如果△ABC的三边所对的角分别为A、B、C，且满足的值．

正确答案

（I）

∵的最小正周期为，且＞0。

∴∴

∴

由≤≤

得的增区间为

（II）由∴

又由

∴在中，

∴

解析

解析已在路上飞奔，马上就到！

知识点

正弦函数的单调性三角函数中的恒等变换应用余弦定理平面向量数量积的运算

题型：简答题

简答题 · 12 分

16．已知函数，三个内角的对边分别为．

（I）求的单调递增区间及对称轴的方程；

（Ⅱ）若，求角的大小．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

正弦函数的单调性正弦函数的对称性三角函数中的恒等变换应用余弦定理

题型：填空题

填空题 · 13 分

16．已知函数，（其中），其部分图像如图1所示。

（1）求函数的解析式；

（2）已知横坐标分别为、、的三点、、都在函数的图像上，求的值。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

同角三角函数间的基本关系由y=Asin（ωx+φ）的部分图象确定其解析式余弦定理

题型：简答题

简答题 · 12 分

19．在中，是角所对的边，是该三角形的面积，且．

（1）求角；

（2）若，求的值．

正确答案

（1）由已知等式得：

，

（2）

解析

解析已在路上飞奔，马上就到！

知识点

同角三角函数间的基本关系三角函数中的恒等变换应用余弦定理

题型：简答题

简答题 · 12 分

16．已知函数　（），且函数的最小正周期为

（1）求函数的解析式；

（2）在△中，角所对的边分别为．若，，且，试求的值。

正确答案

（1）

由，得

∴

（2）由得由，得．

∴，…8分由，得，

再由余弦定理得，

解析

解析已在路上飞奔，马上就到！

知识点

三角函数的周期性及其求法三角函数中的恒等变换应用余弦定理平面向量数量积的运算向量在几何中的应用

题型：简答题

简答题 · 12 分

16．在△ABC中，角A、B、C所对的边分别为a、b、c， q=（，1），p=（，）且．求：

（1）求sin A的值；

（2）求三角函数式的取值范围。

正确答案

解：（1）∵，∴，

根据正弦定理，得，

又，

，，，

又；sinA=

（2）原式，

，

∵，∴，

∴，

∴的值域是．

解析

解析已在路上飞奔，马上就到！

知识点

正弦定理余弦定理三角形中的几何计算平面向量共线（平行）的坐标表示

题型：单选题

单选题 · 5 分

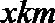
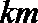
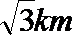
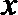
8. 某人向正东方向走后，向右转150°，然后朝新方向走3，结果他离出发点恰好是，那么的值为( )

C或

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

余弦定理

继续学习学习下一知识点

下一知识点 : 余弦定理的应用

百度题库 > 高考 > 理科数学 > 余弦定理

扫码查看完整答案与解析