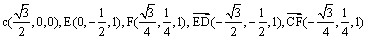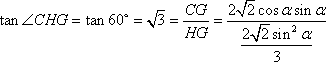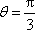- 直线与平面垂直的判定与性质
- 共169题
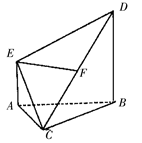
如图,在多面体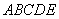
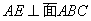
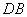
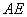
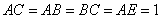
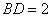
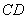
(1)求证:
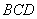
(2)求平面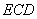
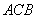
正确答案
见解析。
解析
(1)找BC中点G点,连接AG,FG,
∴F,G分别为DC,BC中点,∴FG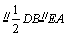
∴四边形EFGA为平行四边形,
∴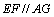
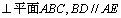
∴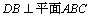
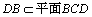
∴平面ABC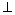
又∵G为BC中点且AC=AB=BC ,∴AG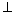
∴AG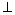
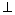
(2)以H为原点建立如图所示的空间直角坐标系
则
设平面CEF的法向量为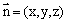
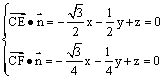
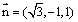
平面ABC的法向量为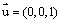
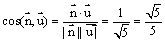
∴平面角ECD和平面ACB所成的锐二面角的余弦值为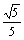
知识点
在如图所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,FC⊥平面ABCD,AE⊥BD,CB=CD=CF。
(1)求证:BD⊥平面AED;
(2)求二面角F-BD-C的余弦值。
正确答案
见解析。
解析
(1)在等腰梯形ABCD中,AB∥CD,∠DAB=60°,CB=CD,
由余弦定理可知
即







(2)
由(Ⅰ)可知





设向量



取




二面角F-BD-C的余弦值为
知识点
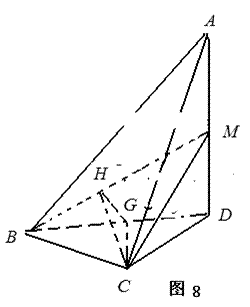
如图,在四面体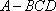
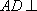
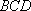
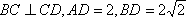
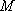
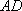
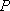
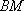
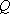
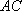
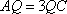
(1)证明: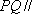
(2)若二面角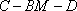
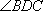
正确答案
见解析。
解析
(1)方法一:如图6,取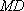
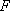
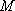
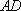
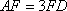
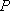
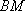
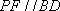
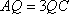
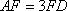
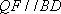
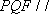
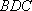
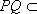
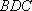
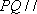
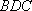
方法二:
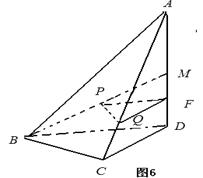
如图7所示,取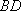

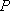
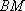
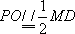
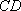
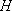
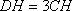
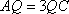
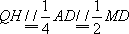
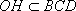
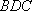
(2)如图8所示,由已知得到面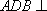
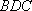
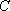
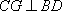

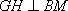
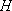
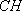
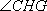
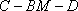
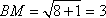
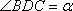
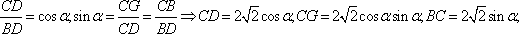
在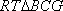
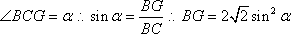
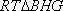
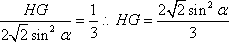
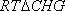
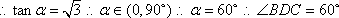
知识点
如图,四棱锥PABCD中,PA⊥平面ABCD,E为BD的中点,G为PD的中点,△DAB≌△DCB,EA=EB=AB=1,PA=
(1)求证:AD⊥平面CFG;
(2)求平面BCP与平面DCP的夹角的余弦值.
正确答案
见解析
解析
知识点
如图,四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点。
(1)证明B1C1⊥CE;
(2)求二面角B1-CE-C1的正弦值;
(3)设点M在线段C1E上,且直线AM与平面ADD1A1所成角的正弦值为
正确答案
见解析
解析
(方法一)
(1)
证明:如图,以点A为原点建立空间直角坐标系,依题意得A(0,0,0),B(0,0,2),C(1,0,1),B1(0,2,2),C1(1,2,1),E(0,1,0)。
易得



所以B1C1⊥CE.
(2)
设平面B1CE的法向量m=(x,y,z),
则
消去x,得y+2z=0,不妨令z=1,可得一个法向量为m=(-3,-2,1)。
由(1),B1C1⊥CE,又CC1⊥B1C1,可得B1C1⊥平面CEC1,
故
于是cos〈m,

从而sin〈m,

所以二面角B1-CE-C1的正弦值为
(3)

设




可取
设θ为直线AM与平面ADD1A1所成的角,则
sin θ=|cos〈

=
于是

所以AM=
(方法二)
(1)
证明:因为侧棱CC1⊥底面A1B1C1D1,B1C1
所以CC1⊥B1C1.
经计算可得B1E=


从而B1E2=
所以在△B1EC1中,B1C1⊥C1E,
又CC1,C1E
所以B1C1⊥平面CC1E,
又CE
(2)过B1作B1G⊥CE于点G,连接C1G.
由(1),B1C1⊥CE,故CE⊥平面B1C1G,得CE⊥C1G,
所以∠B1GC1为二面角B1-CE-C1的平面角。
在△CC1E中,由CE=C1E=

在Rt△B1C1G中,B1G=
所以sin∠B1GC1=
即二面角B1-CE-C1的正弦值为
(3)连接D1E,过点M作MH⊥ED1于点H,可得MH⊥平面ADD1A1,连接AH,AM,则∠MAH为直线AM与平面ADD1A1所成的角。
设AM=x,从而在Rt△AHM中,有MH=

在Rt△C1D1E中,C1D1=1,ED1=

在△AEH中,∠AEH=135°,AE=1,
由AH2=AE2+EH2-2AE·EHcos 135°,得
整理得5x2-

所以线段AM的长为
知识点
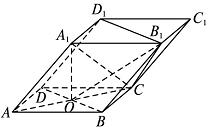
如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,A1O⊥平面ABCD,AB=AA1=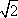
(1)证明:A1C⊥平面BB1D1D;
(2)求平面OCB1与平面BB1D1D的夹角θ的大小。
正确答案
见解析
解析
(1)
证法一:由题设易知OA,OB,OA1两两垂直,以O为原点建立直角坐标系,如图。
∵AB=AA1=
∴OA=OB=OA1=1,
∴A(1,0,0),B(0,1,0),C(-1,0,0),D(0,-1,0),A1(0,0,1)。
由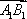
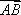
∵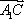
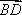
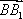
∴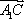
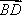
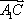
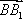
∴A1C⊥BD,A1C⊥BB1,
∴A1C⊥平面BB1D1D。
证法二:∵A1O⊥平面ABCD,∴A1O⊥BD。
又∵ABCD是正方形,∴BD⊥AC,∴BD⊥平面A1OC,∴BD⊥A1C。
又∵OA1是AC的中垂线,∴A1A=A1C=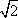
又BB1∥AA1,∴A1C⊥BB1,∴A1C⊥平面BB1D1D。
(2)解:设平面OCB1的法向量n=(x,y,z),
∵
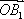
∴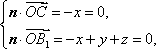
取n=(0,1,-1),
由(1)知,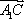
∴cos θ=|cos〈n,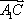
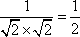
又∵0≤θ≤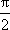
知识点
如图,在四棱锥






(1) 证明:

(2) 求二面角
正确答案
见解析
解析
(1)在直角梯形BCDE中,由DE=BE=1,CD=2,得BD=BC=
由

从而AC⊥平面BCDE,
所以AC⊥DE,又DE⊥DC,从而
DE⊥平面ACD;
(2)方法1
作BF⊥AD,与AD交于点F,过点F作FG∥DE,与AB交于点G,连接BG,由(1)知DE⊥AD,则FG⊥AD,所以∠BFG就是二面角B-AD-E的平面角,在直角梯形BCDE中,由CD2=BC2+BD2,得BD⊥BC,
又平面ABC⊥平面BCDE,得BD⊥平面ABC,从而
BD⊥AB,由于AC⊥平面BCDE,得
AC⊥CD。
在Rt△ACD中,由DC=2,

在Rt△AED中,由ED=1,

在Rt△ABD中,由
得


在△ABE,△ABG中,利用余弦定理分别可得

在△BFG中,

所以,∠BFG=

方法2:以D的原点,分别以射线DE,DC为x,y轴的正半轴,建立空间直角坐标系
由题意知各点坐标如下:




设平面ADE的法向量为
平面ABD的法向量为


由

由

于是
由题意可知,所求二面角是锐角,故二面角B-AD-E的大小为
知识点
如图,在三棱锥









(1)求证:

(2)求

(3)设点





正确答案
见解析
解析
(1)证明:因为 



所以 
又因为 

所以 

又因为 

所以 
因为 

所以 
又因为 
所以 

(2)解:在平面

因为 

所以 

由 




所以以



则





……………… 6分
设平面

因为 

由 
令

设


因为 
所以 
即 
(3)解:因为 

所以 
又因为 
所以 
因为 



所以 
解得 
知识点
如图,在四面体










(1)证明:

(2)若二面角


正确答案
见解析
解析
证明(1)方法一:如图6,取
















方法二:如图7所示,
取













(2)如图8所示,
由已知得到面














在




知识点
如图,在四棱锥P—ABCD中,底面是边长为

(1)证明:MN∥平面ABCD;
(2) 过点A作AQ⊥PC,垂足为点Q,求二面角A—MN—Q的平面角的余弦值。
正确答案
见解析
解析
本题主要考察线面平行的证明方法,建系求二面角等知识点。
(1)如图连接BD.
∵M,N分别为PB,PD的中点,
∴在
又MN
∴MN∥平面ABCD;
(2)如图建系:
A(0,0,0),P(0,0,


N(

设Q(x,y,z),则
∵

由


对于平面AMN:设其法向量为
∵
则

同理对于平面AMN得其法向量为
记所求二面角A—MN—Q的平面角大小为
则
∴所求二面角A—MN—Q的平面角的余弦值为
知识点
扫码查看完整答案与解析