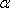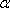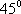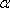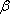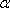- 平面与平面垂直的判定与性质
- 共123题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
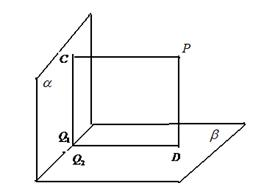
在空间中,过点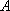
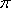
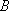
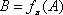
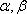
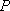
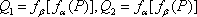
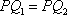
正确答案
解析
设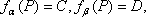
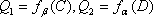
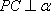
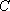
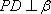
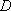
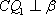
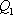
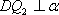
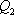
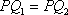
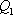
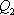
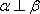
知识点
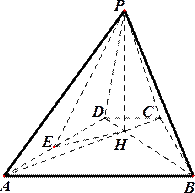
如图,在四面体







(1)若



(2)若二面角





正确答案
见解析
解析
(1)如图所示,设F为AC的中点,由于AD=CD,所以DF⊥AC.
故由平面







故四面体ABCD的体积
(2)如图所示设G、H分别为变CD,BD的中点,则FG//AD,GH//BC,,从而


设E为边AB的中点,则EF//BC,由











在

从而
因





故异面直线

知识点
如图,在五棱锥P—ABCDE中,PA⊥平面ABCDE,AB∥CD,AC∥ED,AE∥BC,∠ABC=45。
,AB=2
(1)求证:平面PCD⊥平面PAC;
(2)求直线PB与平面PCD所成角的大小;
(3)求四棱锥P—ACDE的体积。
正确答案
见解析。
解析
(1) 证明 :在
所以
因此 

又 

又 
所以 
所以 
(2)解法一:
因为 三角形
所以 
因此 
又 
所以点B到平面

由于


所以 
故 

所以B到平面平面

设直线


则
又
所以 
解法二:
由(1)知






又
因此 
因为 
所以 四边形
因为 
所以 
因此 
故 
所以 
因此 
设

则 
解得 
取

又
设



则 
所以 
因此直线PB与平面PCD所成角为
(3)因为
所以 四边形四边形
因为 
所以 
因此 
故 
所以 
又 
所以 四棱锥P—ACDE的体积
知识点
如图,正方形







(1)当点



(2)当平面



正确答案
见解析。
解析
(1)以直线





则




又



∴


(2)设

设


设



取

又由题设,

∴ 
即点




∴ 
知识点
如图,已知四棱锥P-ABCD的底面为等腰梯形,AB∥CD,AC⊥BD,垂足为H,PH是四棱锥的高,E为AD中点。
(1)证明:PE⊥BC;
(2)若∠APB=∠ADB=60°,求直线PA与平面PEH所成角的正弦值。
正确答案
见解析。
解析
以H为原点,HA、HB、HP分别为x、y、z轴,线段
HA的长为单位长,建立空间直角坐标系如图,
则A(1,0,0),B(0,1,0)。
(1)设C(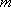

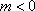
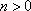
则D(0,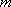

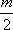
可得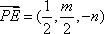
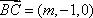
因为
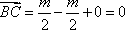
(2)由已知条件可得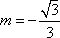
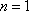
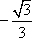
D(0,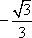

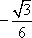
设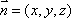
则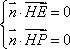
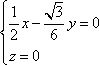
因此可以取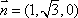
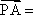
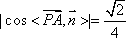
所以直线PA与平面PEH所成角的正弦值为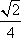
知识点
如图,AB是圆的直径,PA垂直圆所在的平面,C是圆上的点。
(1)求证:平面PAC⊥平面PBC;
(2)若AB=2,AC=1,PA=1,求二面角CPBA的余弦值。
正确答案
见解析
解析
(1)证明:由AB是圆的直径,得AC⊥BC.
由PA⊥平面ABC,BC⊂平面ABC,得PA⊥BC.
又PA∩AC=A,PA⊂平面PAC,AC⊂平面PAC,
所以BC⊥平面PAC.
因为BC⊂平面PBC.
所以平面PBC⊥平面PAC.
(2)解法一:
过C作CM∥AP,则CM⊥平面ABC.
如图,以点C为坐标原点,分别以直线CB,CA,CM为x轴,y轴,z轴建立空间直角坐标系。
因为AB=2,AC=1,所以BC=
因为PA=1,所以A(0,1,0),B(
故


设平面BCP的法向量为n1=(x,y,z),
则
所以
不妨令y=1,则n1=(0,1,-1)。
因为


设平面ABP的法向量为n2=(x,y,z),
则
不妨令x=1,则n2=(1,
于是cos〈n1,n2〉=
所以由题意可知二面角CPBA的余弦值为
解法二:
过C作CM⊥AB于M,
因为PA⊥平面ABC,CM⊂平面ABC,
所以PA⊥CM,故CM⊥平面PAB.
过M作MN⊥PB于N,连接NC,
由三垂线定理得CN⊥PB.
所以∠CNM为二面角CPBA的平面角。
在Rt△ABC中,由AB=2,AC=1,得BC=


在Rt△PAB中,由AB=2,PA=1,得PB=
因为Rt△BNM∽Rt△BAP,
所以

又在Rt△CNM中,CN=

所以二面角CPBA的余弦值为
知识点
如图,在三棱锥









求证:(1)平面

(2)
正确答案
见解析。
解析
证明:(1)∵

∵E.F分别是SA.SB的中点 ∴EF∥AB
又∵EF

同理:FG∥平面ABC
又∵EF


(2)∵平面




∴AF⊥平面SBC 又∵BC
又∵



知识点
已知点G为ABC的重心,过G作直线与AB、AC两边分别交于M、N两点,且


正确答案
解析
M、G、N三点共线
又G为ABC的重心
知识点
扫码查看完整答案与解析