- 直线与平面垂直的判定与性质
- 共169题
1
题型:填空题
|
6.已知α,β表示两个不同的平面,m为平面α内的一条直线,则“α⊥β”是“m⊥β”的( )条件。(填“充分不必要”、“必要不充分”、“充要”或“既不充分也不必要”)
正确答案
必要不充分
解析
解析已在路上飞奔,马上就到!
知识点
充要条件的判定直线与平面垂直的判定与性质平面与平面垂直的判定与性质
1
题型:简答题
|
16.在四棱锥P-ABCD中,∠ACD=90°,∠BAC=∠CAD,PA⊥平面ABCD,E为PD的中点。
(1)求证:平面PAC⊥平面PCD;
(2)求证:CE//平面PAB。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
直线与平面平行的判定与性质直线与平面垂直的判定与性质平面与平面垂直的判定与性质
1
题型:简答题
|
16. 如图,四棱锥







(1)求证:

(2)




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
直线与平面平行的判定与性质直线与平面垂直的判定与性质平面与平面垂直的判定与性质
1
题型:简答题
|
22.如图,在四棱锥









(1)求证:平面

(2)求平面

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
直线与平面垂直的判定与性质平面与平面垂直的判定与性质线面角和二面角的求法
1
题型:简答题
|
18.在多面体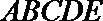
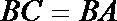
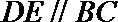
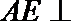
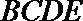
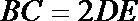
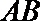
(I)求证: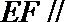
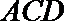
(II)若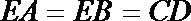
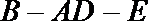
正确答案
证明:(Ⅰ)取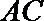
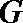
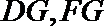
因为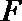
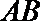
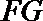
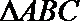
则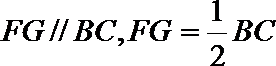
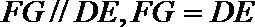
则四边形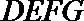
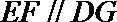
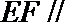
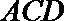
(Ⅱ)过点
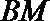
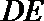
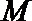
因为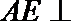
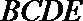
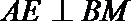
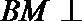
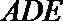
过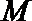
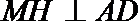

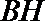
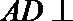
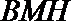
所以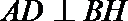
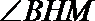
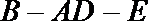
设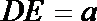
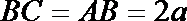
在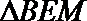
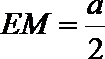
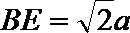
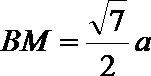
又因为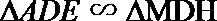
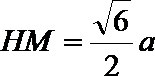
解析
解析已在路上飞奔,马上就到!
知识点
直线与平面平行的判定与性质直线与平面垂直的判定与性质线面角和二面角的求法
下一知识点 : 平面与平面垂直的判定与性质
扫码查看完整答案与解析