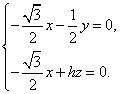- 直线与平面垂直的判定与性质
- 共169题
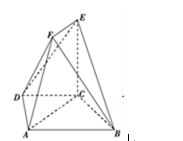
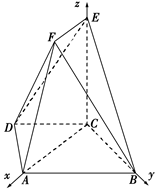
在下图的几何体中,面









(1)求证:

(2)求二面角

正确答案
见解析。
解析
(1)连接



∵


∴

∴四边形
∴


所以

又∵


(2)过
























知识点
在如图所示的几何体中,四边形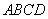
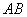
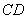
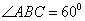
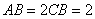
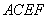
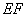
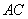
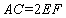
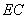
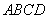
(1)求证: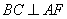
(2)若二面角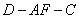
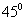
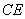
正确答案
见解析。
解析
(1)证明:在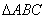
所以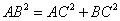
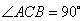
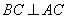
又因为 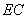
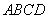
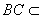
所以 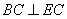
又因为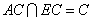
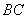
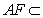
所以 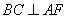
(2)因为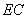
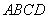
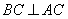
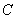
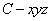
设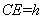
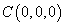
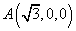
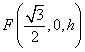
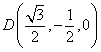
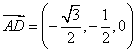
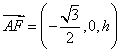
设平面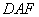
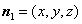
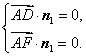
令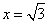
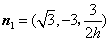
又平面
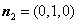
所以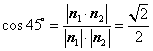
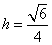
所以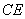
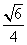
知识点
如图,在四棱锥












正确答案
2
解析
略
知识点
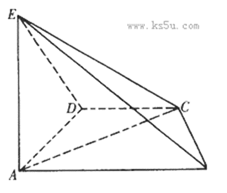
如图,在四棱锥E-ABCD中,EA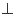
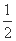

(1)求证:
(2)若AE=AB,求CE与平面ADE所成角的正弦值。
正确答案
见解析。
解析
知识点
设

正确答案
解析
略
知识点
扫码查看完整答案与解析