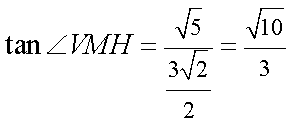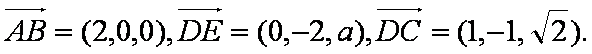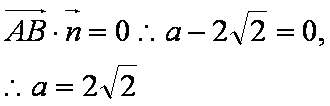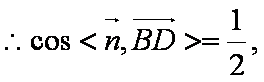- 直线与平面垂直的判定与性质
- 共169题
如图,四棱锥








(1)证明:

(2)求平面

正确答案
见解析
解析
证明:
(1)取





∴



∴









∴




∵





∴

(2)解法一:
连接

建立如图所示的空间直角坐标系,设
则点



设平面




所以平面

所以平面

所以
解法二:
延长



过





令



交




过




所以
所以

知识点
如图,已知四棱锥










(1)证明:平面

(2)求平面

正确答案
见解析。
解析
(1) 证明:



则





(2) 『解法1』:
延长













易求



所以所求角为
因此平面

『解法2』:
以








则





所以

可求得平面
又

可求得平面
则
因此平面


知识点
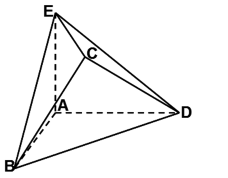
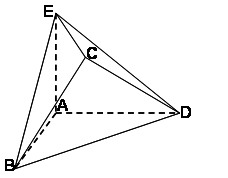
如图,简单组合体ABCDPE,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC.
(1)若N为线段PB的中点,求证:EN⊥平面PDB;
(2)若=,求平面PBE与平面ABCD所成的锐二面角的大小。
正确答案
见解析
解析
(1)证法1:连结AC与BD交于点F,连结NF,
∵F为BD的中点,∴NF∥PD且NF=PD.
又EC∥PD,且EC=PD,(2分)
∴NF∥EC,且NF=EC,∴四边形NFCE为平行四边形,∴NE∥FC.(4分)
∵DB⊥AC,PD⊥平面ABCD,AC⊂面ABCD,∴AC⊥PD.
又PD∩BD=D,∴AC⊥面PBD,∴NE⊥面PDB.(6分)
证法2:以点D为坐标原点,以AD所在的直线为x轴建立空间直角坐标系如图所示:设该简单组合体的底面边长为1,PD=a,
则B(1,1,0),C(0,1,0),P(0,0,a),E(0,1,),N(,,),
∴=(,-,0),=(1,1,-a),=(1,1,0)。
∵·=×1-×1-a×0=0,·=×1-×1+0×0=0,
∴EN⊥PB,EN⊥DB.∵PB、DB⊂面PDB,且PB∩DB=B,∴NE⊥面PDB.(6分)
(2)解法1:连结DN,由(1)知NE⊥面PDB,∴DN⊥NE.
∵=,DB=AD,∴PD=DB,∴DN⊥PB,∴为平面PBE的法向量。
设AD=1,则N(,,),∴=(,,)。
∵为平面ABCD的法向量,=(0,0,),(10分)
设平面PBE与平面ABCD所成的二面角为θ,则cosθ===,
∴θ=45°,即平面PBE与平面ABCD所成的锐二面角为45°.(12分)
解法2:延长PE与DC的延长线交于点G,连结GB,
则GB为平面PBE与平面ABCD的交线.(8分)
∵PD=2EC,∴CD=CG=CB,
∴D、B、G在以C为圆心、以BC为半径的圆上,
∴DB⊥BG.(9分)
∵PD⊥平面ABCD,BG⊂面ABCD,∴PD⊥BG,且PD∩DB=D,∴BG⊥面PDB.
∵PB⊂面PDB,∴BG⊥PB,∴∠PBD为平面PBE与平面ABCD所成的锐二面角的平面角.(10分)
在Rt△PDB中,∵PD=DB,
∴∠PBD=45°,即平面PBE与平面ABCD所成的锐二面角为45°.(12分)
知识点
在三棱锥




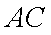


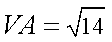



(1)求点

(2)求二面角
正确答案
(1)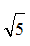

解析
解析:(1)∵




∴






则





在
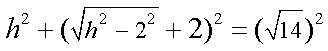




(2)∵







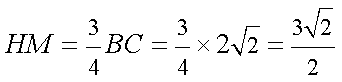
知识点
在几何体ABCDE中,AB=AD=BC=CD=2, 
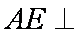
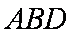
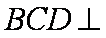
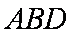
(1)当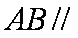
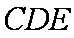
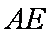
(2)当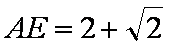
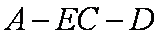
正确答案
见解析
解析
解:(1)设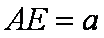
则A(0,0,0),B(2,0,0),D(0,2,0),E(0,0,a),
取BD的中点T,连接CT,AT,则CT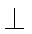
又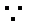
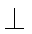
所以CT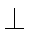
所以CT//AE.
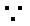

所以CD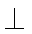
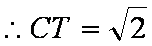
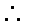
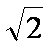
设平面CDE的法向量为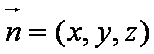
则有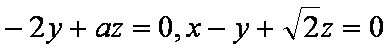
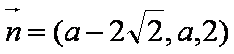
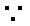
即AE的长为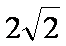
(2)连接AC,当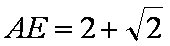
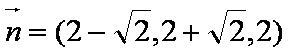
又BD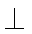
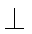
知识点
扫码查看完整答案与解析