- 直线与平面垂直的判定与性质
- 共169题
在直三棱柱




(1)试在棱



(2)当点




正确答案
见解析
解析
解法一:(1)由于平面

所以


而


(2)设



由(1)知



又



在



又因为



所以

解法二:如图


因为


以

则




(1)






又


(2)由(1)知平面

再设平面



所以


故

知识点
如图,几何体














(1)求证:
(2)求二面角
正确答案
见解析
解析
(1)连接




因为





所以四边形

因为




所以
所以
(2)取




以

则
所以
设面

则

令

设面

则

令

则


知识点
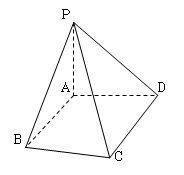
如图,已知
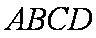
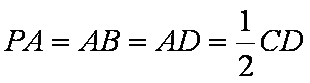
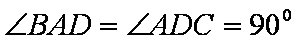
(1)在线段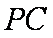
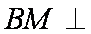

(2)求由面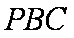
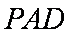
正确答案
(1)M为PC的中点
(2)
解析
(1)M为PC的中点,设PD中点为N,
则MN=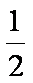
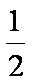
∴ABMN为平行四边形,∴BM//AN,
又PA=AD,∠PAD=90○
∴AN⊥PD,
又CD⊥AN,
∴AN⊥面PCD,
∴BM⊥面PCD
(2)延长CB交DA于E,
∵AB=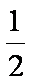
AB//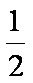
∴AE=AD=PA,∴PD⊥PE
又∴PE⊥CD,∴PE⊥面PCD,
∴∠CPD为二面角C-PE-D的平面角;PD=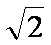
∴tan∠CPD=
知识点
已知在四棱锥P -ABCD中底面ABCD是平行四边形,PA⊥平面ABCD,PA=
(1)求证:PH∥平面GED;
(2)过点F作平面



正确答案
见解析
解析
(1)连接HC,交ED于点N,连结GN,
由条件得:DHEC是矩形,∴N是线段HC的中点,又G是PC的中点,
∴ GN//PH,
又 ∵ GN
∴ PH//平面GED.
(2) 方法1:连结AE,∵

则B(




则E(







设Q(0,0,


设
则

令

设

则



当平面GED⊥平面

得

方法2:
连接BH,则BH//ED,又∵PB//GE,∴平面PBH//平面GED,
设BH与AE交于点K,PK的中点为M,
∵F是PB的中点,∴FM//BK,
∵ABEH是菱形,∴AE⊥BK,
∵PA⊥平面ABCD,∴PA⊥BK ,∴ BK⊥平面PAK.
∴ FM⊥平面PAK,
过M作MQ⊥PK,交PA于Q,设MQ与FM所确定的平面为
∵ED//BH// FM,∴ED//平面


得平面
∵


由
得
知识点
如图,已知斜三棱柱(侧棱不垂直于底面)



(1) 设AC的中点为D,证明

(2) 求侧面
正确答案
见解析。
解析
(1)证明: ∵

∴三角形
又D是斜边AC的中点,∴
∵平面

(2)∵
∴三角形
则
∴
以D为原点,



设平面

则

令



由(1)得A1D⊥面ABC,所以设平面ABC的一个法向量为
设向量


即侧面A1 ABB1 与底面ABC所成二面角的余弦值为
知识点
扫码查看完整答案与解析