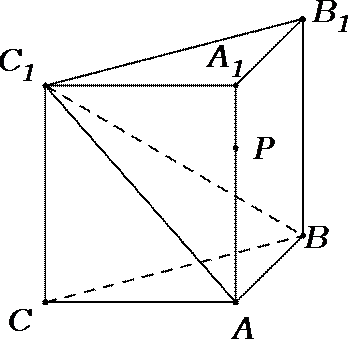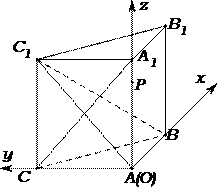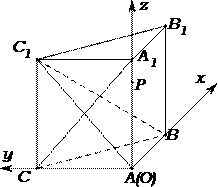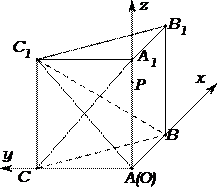- 直线与平面垂直的判定与性质
- 共169题
16.如图,在三棱柱





(1)求证:平面

(2)求证:

正确答案
见解析。
解析
(1)证明:在
在



又点


又








(2)证明:连接
由题意知,点



又





知识点
19.如图,侧棱垂直底面的三棱柱
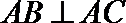
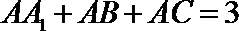
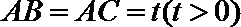
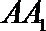
(Ⅰ)当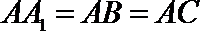
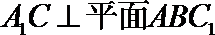
(Ⅱ)试求三棱锥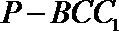
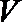
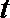
(Ⅲ)若二面角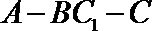
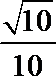
正确答案
(Ⅰ)证法一:∵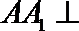
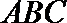
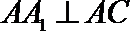
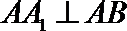
又∵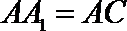
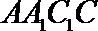
∴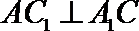
∵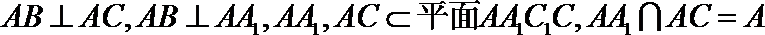
∴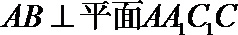
又∵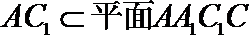
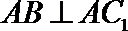
∵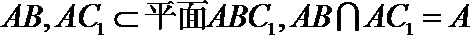
∴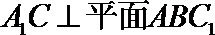
证法二:
∵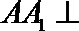
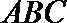
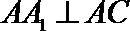
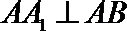
又∵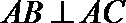
∴分别以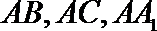
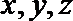
则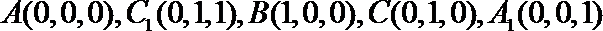
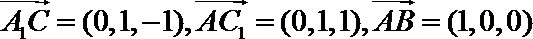
∴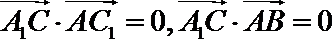
∴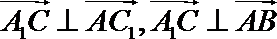
又∵
∴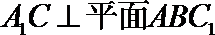
证法三:
∵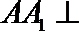
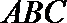
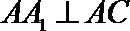
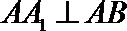
又∵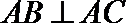
∴分别以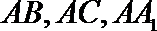
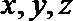
则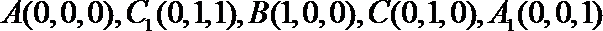
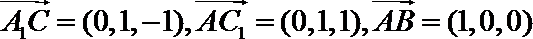
设平面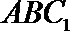
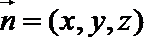
则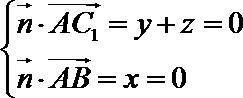
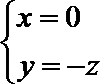
令
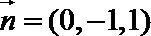
∵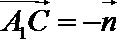
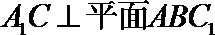
(Ⅱ)∵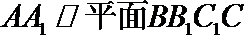
∴点
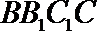
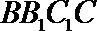
∴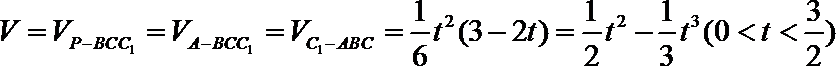
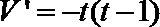
令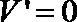
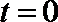
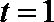
得
∴当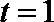
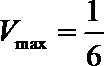
(Ⅲ)
分别以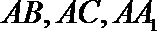
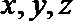
则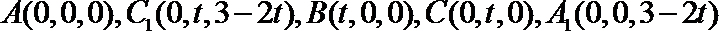
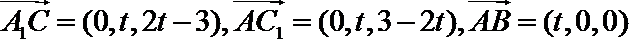
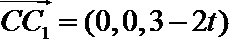
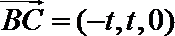
设平面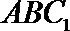
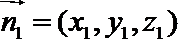
则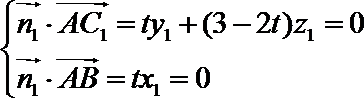
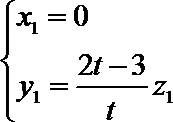
令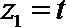
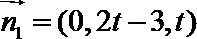
设平面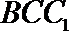
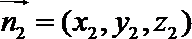
则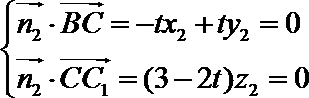
由于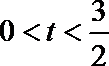
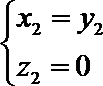
令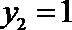
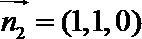
设二面角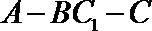
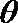
则有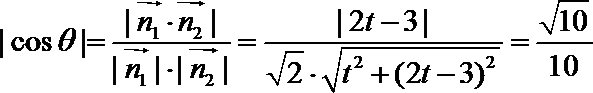
化简得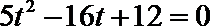
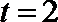
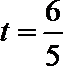
所以当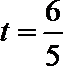
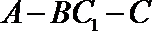
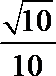
解析
解析已在路上飞奔,马上就到!
知识点
17.如图,简单组合体ABCDPE,其底面ABCD为边长为

(1)若N为线段PB的中点,求证:EN//平面ABCD;
(2)求点

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.
(1)求证:AA1⊥平面ABC;
(2)求二面角A1-BC1-B1的余弦值;
(3)证明:在线段BC1上存在点D,使得AD⊥A1B,并求
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.如图:PA⊥平面ABCD,ABCD是矩形,PA=AB=1,PD与平面ABCD所成角是30°,点F是PB的中点,点E在边BC上移动。
(Ⅰ)点E为BC的中点时,试判断EF与平面PAC的位置关系,并说明理由;

(Ⅲ)当BE等于何值时,二面角P-DE-A的大小为45°。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 如图,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,AB= PA=1,AD=

(I)求证:AF⊥平面PBC;
(II)当BE为何值时,二面角C-PE-D为45o.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.如图,四棱锥







(1)求证:
(2)






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.从平行六面体的8个顶点中任取5个顶点为顶点,恰好构成四棱锥的概率为( )
正确答案
解析
四棱锥的底面可由6个侧面和6个对角面构成,每个底面对应4个四棱锥,故所求概率为P=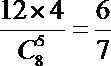
知识点
选做题(14、15题,只能从中选做一题,两题全答的,只计前一题的得分)
14.(参数方程与极坐标)
已知在直角坐标系中曲线









15.(几何证明选讲)
如图,









正确答案
14.
15. 15
解析
解析已在路上飞奔,马上就到!
知识点
7.如图,已知边长为6的正方形







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析