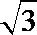- 直线与平面垂直的判定与性质
- 共169题
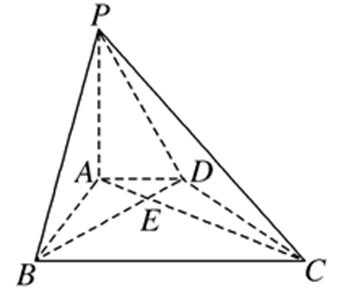
18. 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.
(Ⅰ)证明:PB∥平面AEC;
(Ⅱ)设二面角D-AE-C为60°,AP=1,AD=
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.如图,在底面为直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°,PA⊥平面ABCD,PA=3,AD=2,AB=2,BC=6.
(1)求证:BD⊥平面PAC;
(2)求平面PBD与平面BDA所成的二面角大小.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知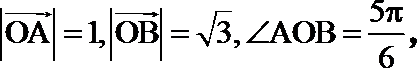
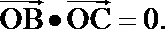
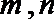
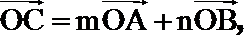
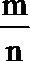
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.如图,在三棱柱





(1)求证:
(2)求棱
(3)在线段


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1,ACC1A1均为正方形,∠BAC=90°,点D是棱B1C1的中点.
(1)求证:A1D⊥平面BB1C1C;
(2)求证:AB1∥平面A1DC;
(3)求二面角D-A1C-A的余弦值.
正确答案
(1)证明:因为侧面均为正方形,
所以
所以


因为


又因为



因为


(2)
证明:连结



因为


又



所以
因为



所以

(3)解: 因为侧面


所以

设


设平面




取

又因为




因为二面角
所以,二面角

解析
解析已在路上飞奔,马上就到!
知识点
7.已知正方形ABCD的对角线AC与BD相交于E点,将
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.设

①若



②若




③设






④直线



其中所有真命题的序号是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数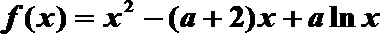
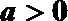
(1)当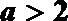
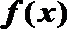
(2)当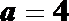
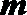
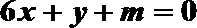

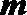
(3)设定义在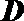
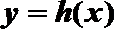
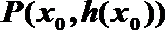
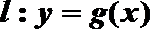
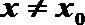
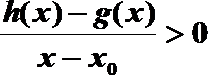
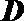
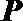
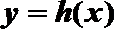
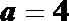

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18. AB为圆O的直径,点E、F在圆上,AB∥EF,矩形ABCD所在平面与圆O所在平面互相垂直,已知AB=2,BC=EF=1.
(Ⅰ)求证:BF⊥平面DAF;
(Ⅱ)求平面ADF与平面CDFE所成的二面角的余弦值.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.如图,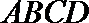
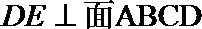
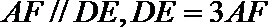
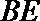
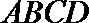
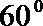
(1)求二面角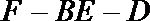
(2)设点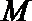
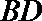
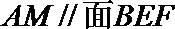
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析