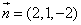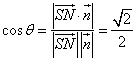- 直线与平面垂直的判定与性质
- 共169题
18.如图,四棱锥



(1)求证:平面

(2)当



(3)在(2)的条件下若F是PD的靠近P的一个三等分点,求二面角A-EF-D的余弦值.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.如图所示,在三棱锥








(1)证明
(2)求直线

正确答案
(1)以点




则

于是
因为


(2)由(1)可得,
于是

设平面
则





设直线


则



解析
解析已在路上飞奔,马上就到!
知识点
18.已知某几何体的直观图和三视图如下图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形.

(1)证明:BN⊥平面C1B1N;
(2)求二面角
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.四棱锥







(1)求四棱锥
(2)不论

(3)若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
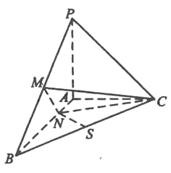
19.已知三棱锥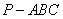
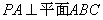
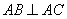
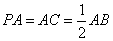
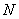
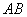
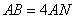
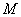
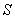
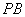
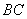
(1)求证: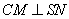
(2)求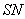
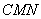
正确答案
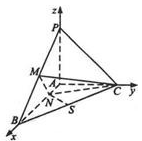
设PA=1,以A为原点,射线AB,AC,AP分别为x,y,z轴正向建立空间直角坐标系如图所示:
则P(0,0,1),C(0,1,0),B(2,0,0),M(1,0, ),N( ,0,0),S(1, ,0)
(1)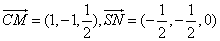
因为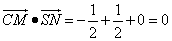
所以CM⊥SN
(2)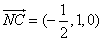
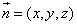
则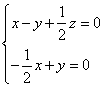
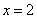
因为
所以SN与片面CMN所成角为45°。
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析