- 函数的概念及其构成要素
- 共2084题
已知函数

(1)若曲线
(2)当

正确答案
见解析
解析
(1)函数h(x)定义域为{x|x≠-a},…………………………………………………1分
则





(2)记






令















单调递减区间为



① 当




② 当






③当




综上所述,当





知识点
已知函
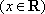
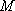
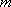
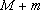
正确答案
2
解析
略
知识点
已知函数


正确答案
解析
略
知识点
已知函数

(1)试讨论

(2)当







正确答案
见解析
解析
(1)解:由已知

由


因为


所以在区间



故


(2)证明:由题意可得,当



即 
所以

因为


所以

所以

令



所以


所以
知识点
在平面直角坐标系中,横坐标、纵坐标均为整数的点称为整点,如果函数



① 



其中是一阶整点函数的是( )
正确答案
解析
略
知识点
扫码查看完整答案与解析