- 函数的概念及其构成要素
- 共2084题
已知实数

(1)当

(2)当

(3)求实数



正确答案
(1)2(2)递增(3)
解析
解析:易知


(1)



(2)







设

所以

(3)

从而原问题等价于求实数

恒有
①当





从而
②当




由


③当




由


④当


由


综上,
知识点
函数f(x)=|x﹣2|﹣lnx在定义域内零点的个数为( )
正确答案
解析
由题意,函数f(x)的定义域为(0,+∞);
由函数零点的定义,f(x)在(0,+∞)内的零点即是方程|x﹣2|﹣lnx=0的根.
令y1=|x﹣2|,y2=lnx(x>0),在一个坐标系中画出两个函数的图象:
由图得,两个函数图象有两个交点,
故方程有两个根,即对应函数有两个零点.
故选C.
知识点
方程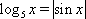
正确答案
解析
略
知识点
如图,设







(1)求点

(2)若

正确答案
(1)
解析
解析:(1)当

所以
所以,点B的坐标是(0,1) ……………………………………………………2分
又


(2)由


又





所以,

知识点
已知函数

正确答案
解析
略
知识点
扫码查看完整答案与解析















