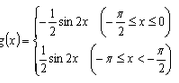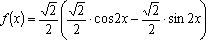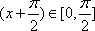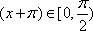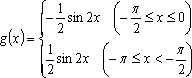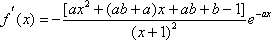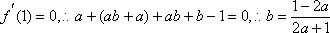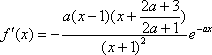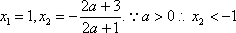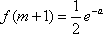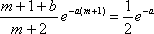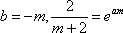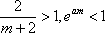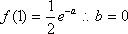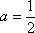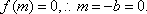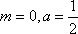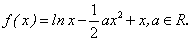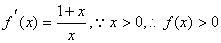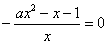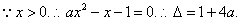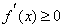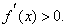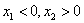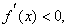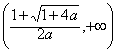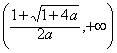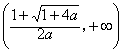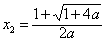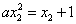- 函数的概念及其构成要素
- 共2084题
已知函数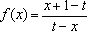

(1)当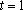
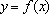
(2)设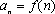
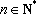
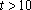
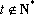
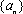
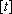

(3)利用函数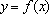
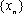
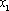
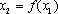
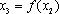
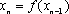
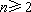
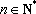
在上述构造过程中,若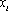
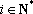
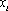
若取定义域中的任一值作为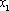
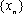

正确答案
见解析
解析
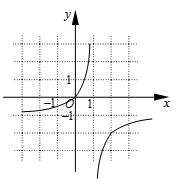
(1)当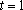
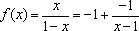
图像如图(2分)
基本性质:(每个2分)
奇偶性:既非奇函数又非偶函数;
单调性:在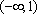
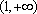
零点: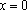
最值:无最大、小值,(6分)
(2)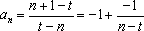
当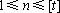
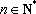
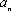
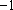
当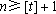
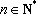
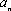
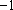
因此,数列中的最大项为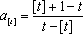
最小项为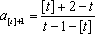
(3)由题意,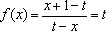
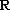
亦即当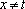
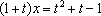
由于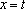
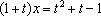
因此对任意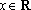
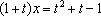
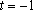
知识点
设函数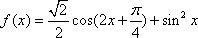
(1)求函数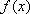
(2)设函数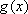
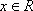
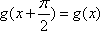
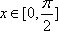
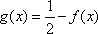
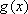

正确答案
(1)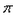
解析
解析: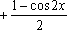
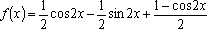
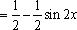
(1)函数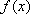
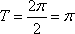

(2)当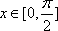
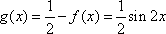
当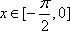
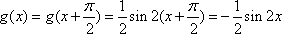
当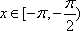
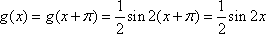
得函数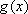
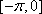
知识点
设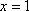
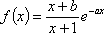
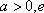
(1)求
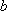

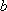
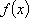
(2)若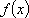
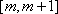
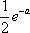
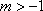
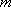

正确答案
见解析。
解析
(1)
由已知有:
从而
令
当
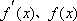
从上表可知: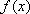
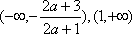
在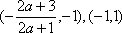
(2)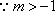
①当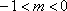
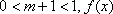
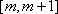
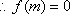
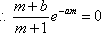
解得
又
故此时的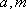
②当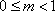
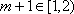
将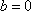
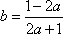
又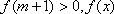
③当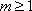
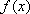
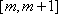
又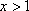
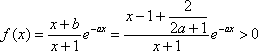
∴此时的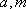
综上所述
知识点
设函数



(1)证明:
(2)当


(3)证明:

正确答案
见解析
解析
(1)证明:设
当





即函数



因为


即

(2)解:当

用数学归纳法证明如下:
①当

②假设当


令

因为对任意的正实数

由归纳假设知,
即


因为

从而对任意

即对任意

这就是说,当


由①、②知,当

(3)先证对任意正整数

由(2)知,当


令


再证对任意正整数

要证明上式,只需证明对任意正整数

即要证明对任意正整数

①当

②假设当

即
则
因为
所以
这说明当
由①、②知,对任意正整数
综上可知,对任意正整数

知识点
已知函数
(1)求函数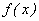
(2)是否存在实数a,使得函数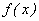
正确答案
见解析
解析
(1)解:函数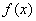

①当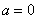
∴函数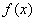
②当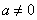
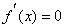
(i)当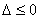
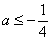
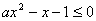
∴函数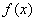
(ii)当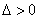
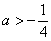
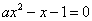
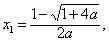
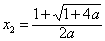
若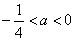
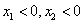
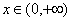
∴函数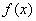
若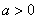
此时,当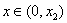
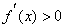
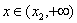
∴函数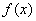
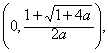
综上所述,当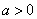
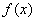
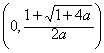
为
当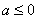
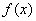
(2)解:由(1)得当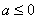
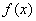
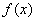
当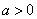
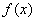
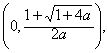
则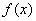
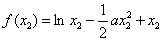
而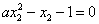
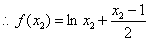
设函数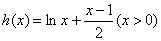
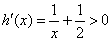
则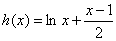
又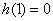
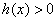
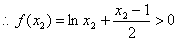
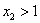
即在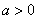
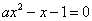
设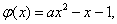
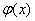
轴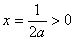
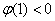
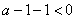
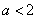
故实数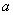
说明:若采用下面的方法求出实数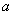
(i),由于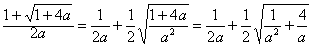
而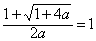
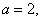
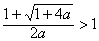
从而实数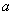
(ii)直接解不等式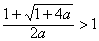
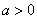
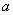
(0,2)。
知识点
扫码查看完整答案与解析