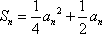- 函数的概念及其构成要素
- 共2084题
已知函数
(1)求函数
(2)求函数

正确答案
(1)
解析
解析:(1)
所以函数

(2)
∵



∴
另解:
∵


∴

知识点
已知函数

(1)判断函数
(2)求



正确答案
见解析
解析
解析:(1)f(x)的定义域为
f(-x)=log2

所以,f(x)为奇函数. ………………………………………..6分
(2)由y=

所以,f -1(x)= 

因为函数
所以,

所以,log2k=

从而,k
知识点
已知函数
(1)求函数


(2)如果当




(3)对任意的



正确答案
见解析
解析
解析:(1)令


对任意
所以函数
另证:对任意
所以函数
(2)由


因为


又因为


且


故






所以

(3)假设存在
即

解得

下证:
证明:

∴

所以存在

另证:要证明





∴
所以存在
知识点
已知函数


(1)求实数
(2)已知结论:若函数








正确答案
见解析
解析
解:(1)



当



当







(2)令
则





使得












故对任意
知识点
设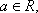
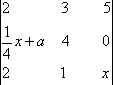
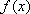

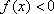
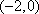
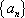

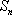
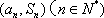
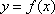
(1)求函数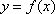
(2)若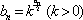
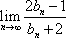
(3)令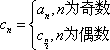
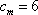
正确答案
见解析
解析
(1)由条件可知,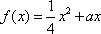
因为关于
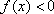
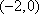
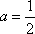
即函数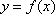
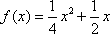
(2)因为点列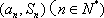
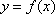
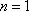
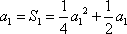
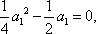
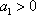
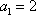
当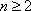
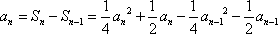
化简得: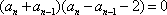
因为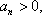
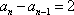
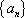
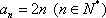
则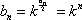
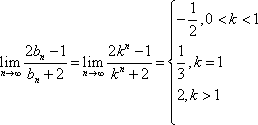
(3)在数列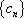
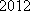

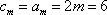
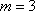

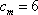
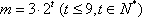
所以,满足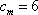
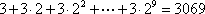
知识点
扫码查看完整答案与解析