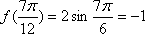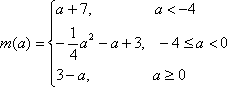- 函数的概念及其构成要素
- 共2084题
已知函数

(1)求
(2)若 

正确答案
见解析。
解析
(1)








则 
(2)由已知得

则

知识点
已知函数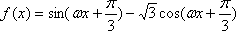
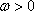
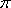
(1)求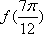
(2)若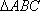
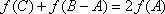
正确答案
见解析。
解析
(1)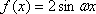
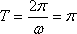
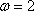
(2)由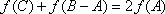
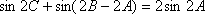
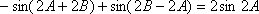
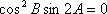
所以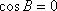
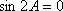
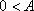
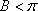
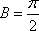
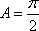
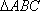
知识点
已知函数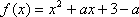
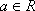
(1)求
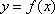
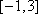
(2)当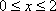
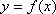

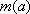
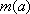

(3)对于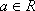
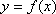
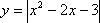
正确答案
见解析
解析
(1)函数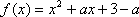
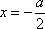
因为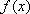
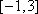
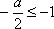
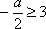
故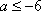
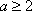
(2)当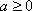
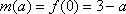
当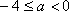
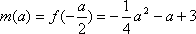
当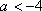
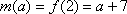
所以,
分段讨论并比较大小得,当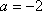
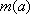
(3)公共点的横坐标
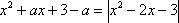

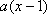
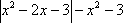
设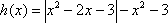
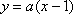
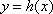
当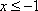
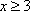
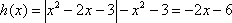
解方程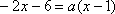
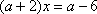
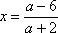
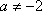
当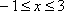
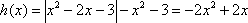
解方程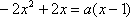
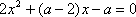
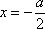
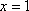
研究结论及评分示例:(满分6分)
结论1:无论
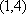
结论2:(对某些具体的
当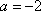
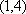
当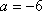
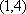
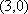
当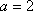
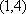
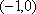
(对每一个具体的
结论3:当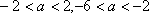
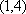
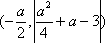
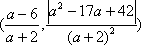
结论4:叙述完整,结论正确,给满分.具体包括下面几个方面:
当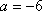
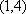
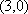
当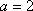
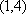
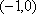
当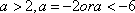
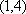
当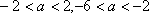
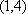
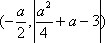
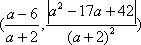
知识点
定义:对函数





(1) 判断函数

(2) 若函数

(3) 已知函数


正确答案
见解析
解析
(1)若存在


……………………………. 2分



“k性质函数”。 ……………………………. 4分
(2)由

即


当

当




综上,
……………………………. 10分
(3)由条件存在




……………………………. 12分

令
则


……………………………. 16分
知识点
已知函数
(1)求函数
(2)在△





正确答案
见解析。
解析
(1)
∵
∴
∴函数
(2)
∴


在


∴
解得
∵

知识点
扫码查看完整答案与解析