- 圆锥曲线中的探索性问题
- 共76题
设点P是曲线C:x2=2py(p>0)上的动点,点P到点(0,1)的距离和它到焦点F的距离之和的最小值为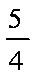
(1)求曲线C的方程;
(2)若点P的横坐标为1,过P作斜率为k(k≠0)的直线交C于点Q,交x轴于点M,过点Q且与PQ垂直的直线与C交于另一点N,问是否存在实数k,使得直线MN与曲线C相切?若存在,求出k的值;若不存在,请说明理由。
正确答案
见解析。
解析
(1)依题意知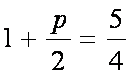
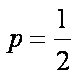
所以曲线
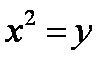
(2)由题意直线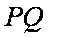
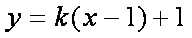
联立方程组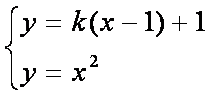
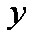
得
所以得直线
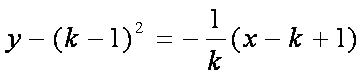
代入曲线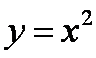
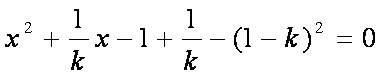
解得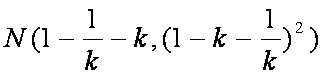
所以直线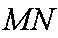
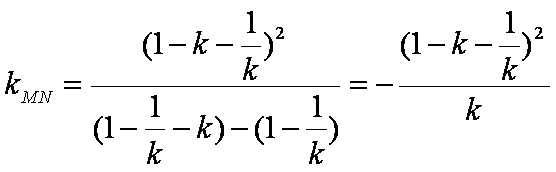
过点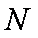
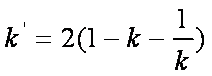
由题意有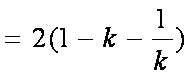
解得
故存在实数
知识点
已知





(1)求点P的轨迹方程;
(2)是否存在定直线

正确答案
(1)y2=x(2)x=
解析
(1)设B(0,t),设Q(m,0),t2=







2










(2)由(1),点P的轨迹方程是y2=x;设P(y2,y),


L=2
=2

若a为常数,则对于任意实数y,L为定值的条件是a-





知识点
已知椭圆





(1)求
(2)设斜率不为









正确答案
见解析
解析
解析:(1)设
和

且




(2)设直线






设切点







化简并整理得


知识点
如图,两条相交线段






(1)若


(2)探究:是否存在常数


正确答案
见解析
解析
(1)由
解得

因为

设

化简得
又


因为


(2)设






若存常数



①当



即
即
即
所以,存常数


②当

故,存常数


知识点
已知椭圆





(1)求该椭圆的标准方程;
(2)当点













正确答案
见解析
解析
(1)由










故椭圆的标准方程为 
(2)设

则


动点


由
设



因为点


故
所以







知识点
扫码查看完整答案与解析