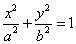- 圆锥曲线中的探索性问题
- 共76题
已知椭圆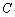
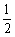
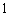
(1)求椭圆
(2)是否存在与椭圆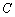
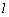
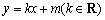
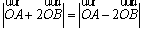
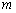
正确答案
见解析
解析
(1)设椭圆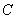
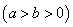
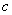
依题意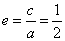
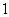
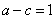
解得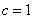
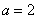
所以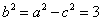
所以椭圆
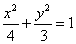
(2)解:存在直线
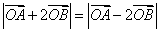
由
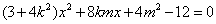
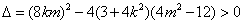
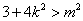
设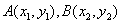
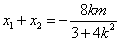
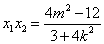
若
即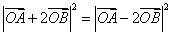
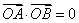
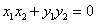
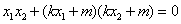
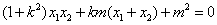
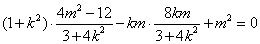
化简得,
将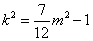

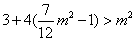
解得,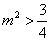
又由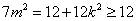
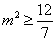
从而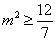
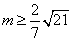
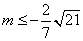
所以实数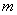
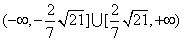
知识点
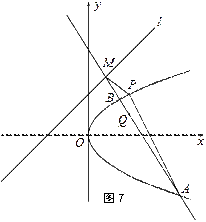
如图7,直线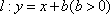
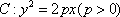
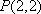
物线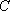
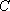
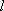

(1)求直线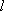
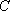
(2)过点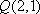
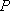
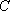
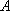

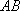
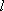
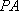
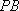
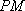
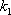
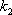
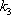
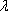
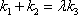
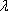
正确答案
见解析。
解析
(1)(法一)

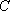
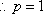
设与直线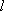
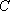
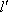
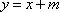
由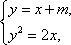
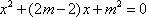
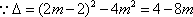

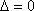
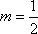
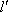
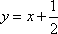

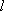


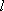

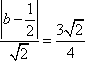

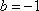


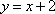

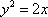
(法二)

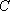
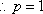


设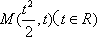
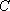
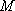
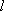

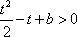
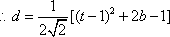
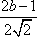
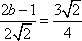
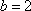
因此,直线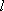
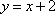
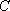
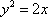
(2)
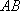

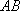
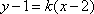

由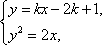
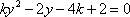
设点
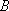
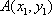
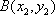
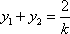

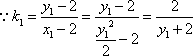

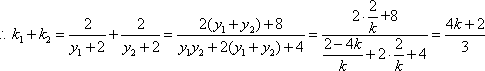
由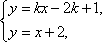
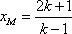
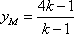
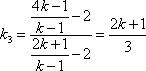
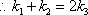
因此,存在实数
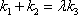
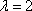
知识点
已知点






(1)求曲线
(2)斜率为








(3)试问:是否存在一个定圆


正确答案
见解析
解析
(1)由题知,有
化简,得曲线

(2)∵直线


∴可设直线

联立方程组

又交点为
∴
∴
(3)答:一定存在满足题意的定圆
理由:∵动圆

∴两圆的圆心之间距离
又



记曲线


∴若定圆的圆心


∴定圆

知识点
已知抛物线的方程为




(1)求抛物线的方程;
(2)已知


(3)设点B、C是抛物线上的动点,点D是抛物线与
正确答案
见解析。
解析
(1)
设点A(3,-1)关于直线

则

把点

所以抛物线的方程为
(2)∵
∴抛物线的准线为
过点M作准线的垂线,垂足为A,由抛物线的定义知
∴

即当点M为过点P所作的抛物线准线的垂线与抛物线的交点时,
∴

(3)BC所在的直线经过定点,该定点坐标为
令
设

则

∵

直线BC的方程为
即
所以直线BC经过定点
知识点
设椭圆
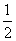
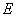
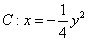
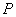
(1)求直线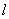
(2)椭圆上是否存在点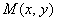
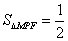
正确答案
见解析。
解析
(1)抛物线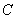
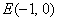
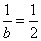
所以,
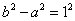

因此,所求椭圆的方程为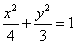
(2)椭圆的右焦点为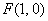
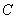


① 若
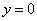
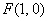
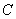
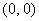
的方程为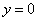
② 若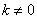

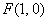
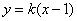
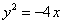
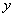
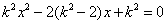
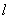
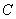
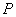
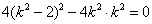
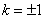
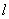
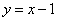


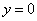
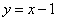

可求出点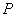
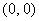
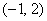
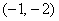
①若点
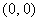
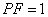
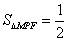
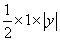

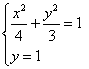
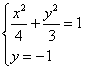
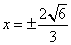
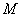
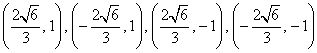
②若点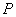
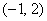
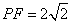
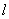
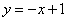
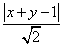
于是有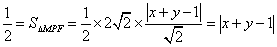
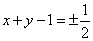
与(*)式联立: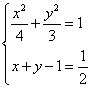

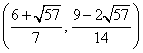
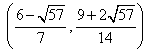


③ 若点
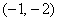
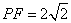
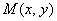

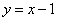
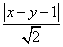
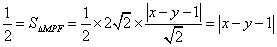
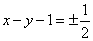
与(*)式联立: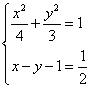

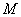
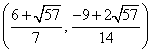
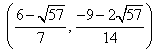
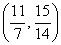
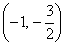
综合①②③,以上12个点各不相同且均在该椭圆上,因此,满足条件的点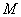
知识点
扫码查看完整答案与解析