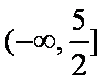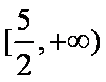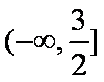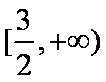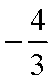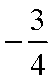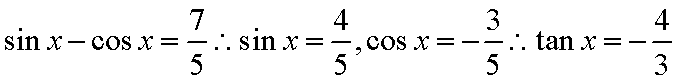- 任意角的概念
- 共691题
已知正实数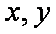
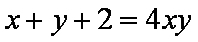
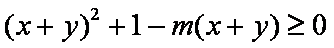
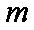
A
B
C
D
正确答案
解析
因为正实数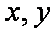
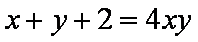
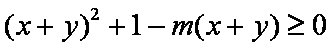
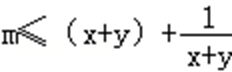
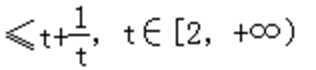
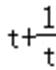
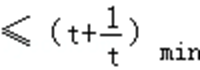
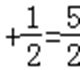
知识点
在△ABC中，
（1）求cos C；
（2）设
正确答案
见解析
解析
（1）∵cosB=
∴sinB=
∵C=π﹣（A+B），A=
∴cosC=﹣cos（
（2）根据正弦定理
再根据余弦定理得：AB2=9+5﹣2×3×
则AB=2
知识点
过抛物线
正确答案
解析
知识点
A
B
C
D
正确答案
解析
知识点
已知
（1）最小正周期及对称轴方程；
（2）已知锐角
正确答案
见解析
解析
（1）
（2）由
由余弦定理得
设
知识点
已知四棱锥
线段AB，BC的中点，
（1）证明：PF⊥FD；
（2）在PA上找一点G，使得EG∥平面PFD；。
（3）若
正确答案
见解析
解析
解析：（1）证明：连接AF，则AF＝，DF＝，
又AD＝2，∴DF2＋AF2＝AD2，
∴DF⊥AF，又PA⊥平面ABCD，
∴DF⊥PA，又PA∩AF＝A，
（2）过点E作EH∥FD交AD于点H，则EH∥平面PFD且AH＝AD。
再过点H作HG∥DP交PA于点G，则HG∥平面PFD且AG＝AP，
∴平面EHG∥平面PFD。
∴EG∥平面PFD。
从而满足AG＝AP的点G为所求。 ………………8分
（3）建立如图所示的空间直角坐标系，因为PA⊥平面ABCD ，所以
又有已知得
设平面
得
所以
又因为
所以
易得
所以
由图知，所求二面角
知识点
已知空间直角坐标系0-
正确答案
解析
由柯西不等式，设
知识点
已知方程
正确答案
解析
∵方程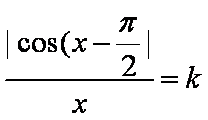
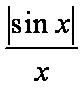
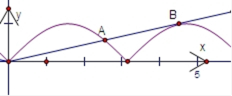
∴函数y=|sinx|和函数y=kx在（0，+∞）上有两个
函数y=|sinx|和函数y=kx在（0，π）上有一个交点A（a，sina），
在（π，2π）上有一个切点B（b，sinb）时满足题意，a，b是方程的根。
当x∈（π，2π）时，f（x）=|sinx|=-sinx，f′（x）=-cosx，
∴在B处的切线为y-sinb=f′（b）（x-b），将x=0，y=0代入方程，得sinb=-bcosb，
∴
∴
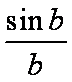
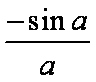
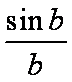
知识点
已知
A
B
C
D
正确答案
解析
知识点
已
A
B
C2
D-2
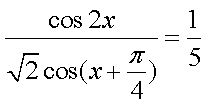
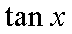
正确答案
解析
解：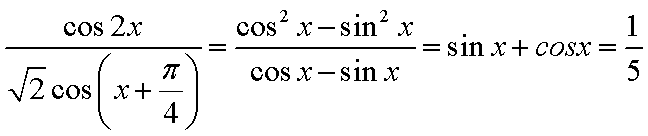
平方可得
可知
知识点
扫码查看完整答案与解析