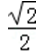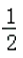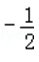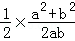- 任意角的概念
- 共691题
把函数y=sinx（x∈R）的图象上所有点向左平行移动
A
B
C
D
正确答案
解析
由y=sinx的图象向左平行移动
再把所得图象上所有点的横坐标缩短到原来的
知识点
已知
A-1
B
C
D1
正确答案
解析
【解析一】
【解析二】
知识点
如图，A, B是海平面上的两个小岛，为测量A, B两岛间的距离，测量船以15海里/小时的速度沿既定直线CD航行，在t1时刻航行到C处，测得∠ACB=75°，∠ACD=120°，1小时后，测量船到达D处，测得∠ADC=30°，∠ADB=45°，求A, B两小岛间的距离.(注：A、B、C、D四点共面)
正确答案
解析
解析：由已知得
在
∴
在
∴
在
故两小岛间的距离为
知识点
已知
（1）
（2）
正确答案
见解析。
解析
（1）
即
（2）
（或者
知识点
在△ABC中，A、B为锐角，角A、B、C所对的边分别为a、b、c，且sinA=
（1）求A+B的值；
（2）若a-b=
正确答案
（1）
（2）a=
解析
（1）∵△ABC中，A、B为锐角，
∴A+B∈（0，π），
又sinA=
∴cosA=
∴cos（A+B）=cosAcosB﹣sinAsinB=
∴A+B=
（2）∵sinA=
∴由正弦定理
∴a=
∴b=1，a=
又C=π﹣（A+B）=π﹣
∴c2=a2+b2﹣2abcosC=2+1﹣2×1×
∴c=
综上所述，a=
知识点
在△ABC中，角A，B，C所对边长分别为a，b，c，若a2+b2=2c2，则cosC的最小值为
A
B
C
D
正确答案
解析
因为a2+b2=2c2，
所以由余弦定理可知，c2=2abcosC，
cosC=
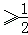
知识点
在直角坐标系xOy中，直线l的参数方程为
正确答案
-3
解析
略
知识点
已知a，b，c分别为ΔABC三个内角A，B，C的对边，且满足
（1）求B；
（2）若ΔABC的面积为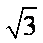
正确答案
（1）B=
（2）
解析
（1）由正弦定理得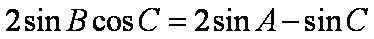
在
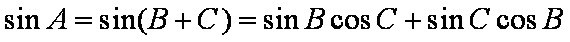
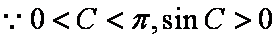
（2）
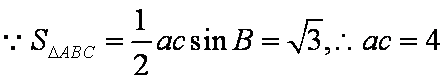
由余弦定理得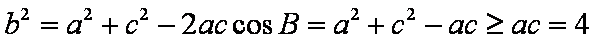
当且仅当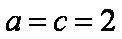
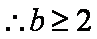
知识点
如图，已知AB为圆O的一条直径，以端点B为圆心的圆交直线AB于C、D两点，交圆O于E、F两点，过点D作垂直于AD的直线，交直线AF于H点.
（1）求证：
（2）若AC=2，AF=2 ,求
正确答案
见解析
解析
解析：（1）因为
又
故
所以，
（2）因为
所以
又
则
连接
知识点
在
A
B
C
D
正确答案
解析
由
因为
知识点
扫码查看完整答案与解析