任意角的概念
共691题

· 任意角的概念

任意角的概念
共691题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 12 分

在中，角、、的对边分别为、、，且。

（1）求角的大小；

（2）若，，求、的值。

正确答案

见解析

解析

（1）由正弦定理得

所以

因为，故

所以

（2）由，得

由条件，，

所以由余弦定理得

解得

知识点

任意角的概念

题型：简答题

简答题 · 12 分

已知向量与为共线向量，且

（1）求的值

（2）求的值

正确答案

（1）（2）

解析

解析：（1）∵m与n为共线向量，∴

即

（2）

又

因此，

知识点

任意角的概念

题型：简答题

简答题 · 12 分

第30届夏季奥运会将于2012年7月27日在伦敦举行, 当地某学校招募了8名男志愿者和12名女志愿者.将这20名志愿者的身高编成如下茎叶图(单位:cm):

若身高在4500px以上(包括4500px)定义为“高个子”, 身高在4500px以下(不包括4500px)定义为“非高个子”, 且只有“女高个子”才能担任“礼仪小组”.

(1) 如果用分层抽样的方法从“高个子”和“非高个子”中抽取5人,再从这5人中选2人,那么至少有一人是“高个子”的概率是多少?

(2) 若从所有“高个子”中选3名志愿者, 用X表示所选志愿者中能担任“礼仪小组”的人数, 试写出X的分布列,并求X的数学期望.

正确答案

解析

知识点

任意角的概念

题型：简答题

简答题 · 12 分

已知 a、b、c为斜三角形ABC的三边，A、B、C为三边所对的角，，，若，，求的值。

正确答案

解析

由知，a2+b2=t2·c2，………………………………………………2′

由于△ABC为斜△，∴t2≠1 …………………………………………………3′

=………………………………12′

知识点

任意角的概念

题型：简答题

简答题 · 12 分

已知定点A(1，0), B为x轴负半轴上的动点，以AB为边作菱形ABCD,使其两对角线的交点恰好落在y轴上.

（1）求动点D的轨迹五的方程.

（2）若四边形MPNQ的四个顶点都在曲线E上，M，N关于x轴对称，曲线E在M点处的切线为l，且PQ//l

①证明直线PN与QN的斜率之和为定值；

②当M的横坐标为，纵坐标大于O,=60°时，求四边形MPNQ的面积。

正确答案

见解析。

解析

（1）设，则由于菱形的中心在轴上，顶点在轴上，所以，，而，所以，.

又，所以，即.

而不可能在轴上，所以顶点的轨迹的方程为. (5分)

（2）①设，，(不妨令)，则，

则，

同理，，

而，

因为，所以，因此即，

所以，即直线与的斜率之和为定值. (8分)

②因为点横坐标为，且纵坐标大于0，所以，.

由于，且轴，所以平分，

而，所以，.

从而直线，即；

直线，即.

由消去并整理得，

所以，即.

同理消去并整理得.

所以，即.

因此为所求. (12分)

知识点

任意角的概念

题型：简答题

简答题 · 12 分

如图，在四面体中，平面平面，90°。，，分别为棱，，的中点。

（1）求证：平面；

（2）求证：平面平面。

正确答案

见解析

解析

证明：（1）因为，分别为棱，的中点，

所以，

又平面，平面，

故平面，

（2）因为，分别为棱，的中点，所以，

又°，故，

因为平面平面，平面平面，且平面，

所以平面，

又平面，

平面平面，

知识点

任意角的概念

题型：填空题

填空题 · 5 分

函数的定义域为(0,),则函数f(x)的值域为

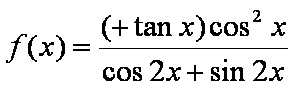
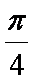
正确答案

解析

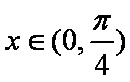
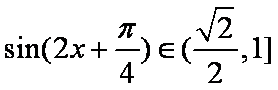
因为，所以，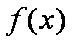

所以的值域为.

知识点

任意角的概念

题型：简答题

简答题 · 12 分

已知a，b，c分别是的三个内角A，B，C的对边，

（1）求A的大小；

（2）当时，求的取值范围。

正确答案

（1）（2）

解析

解析：（1）△ABC中，∵，由正弦定理，得：，

即 2sinBcosA=sinAcosC+sinCcosA，故2sinBcosA=sin（A+C）=sinB，…（4分）

（2）由正弦定理得

，

知识点

任意角的概念

题型：填空题

填空题 · 5 分

如图，在△ABC中，，，，点在边上，45°，则的值为。

正确答案

解析

略

知识点

任意角的概念

题型：单选题

单选题 · 5 分

把函数图象上所有点的横坐标伸长为原来的2倍（纵坐标不变），再把所得函数的图象向右平移个单位，得到图象的解析式为

Ay=5cosx

By=5cos4x

Cy=－5 cosx

Dy=－5 cos4x

正确答案

解析

略

知识点

任意角的概念

继续学习学习下一知识点

下一知识点 : 终边相同的角

百度题库 > 高考 > 理科数学 > 任意角的概念

扫码查看完整答案与解析