任意角的概念
共691题

· 任意角的概念

任意角的概念
共691题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 5 分

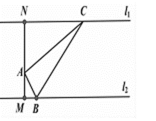
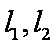
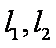
如图，A是两条平行直线之间的一个定点，且A到的距离分别为AM=1，AN=2，设△ABC的另两个顶点B，C分别在上运动，且AB<AC，，则以下命题中。

①△ABC是直角三角形；

②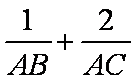的最大值为；

③S代表图形面积，则(S四边形MBCN)min=(S△ABC)min+(S△AMB+S△ACN)min；

④设△AMB的周长为yl，△ACN酌周长为y2，则(y1+y2)min=10。

正确的命题是。（填正确命题的序号）

正确答案

①②④

解析

略

知识点

任意角的概念

题型：简答题

简答题 · 12 分

在△中，角、、的对边分别为、、，，。

（1）求证：；

（2）若△的面积，求的值。

正确答案

见解析

解析

（1）证明：因为，由正弦定理得

，

所以

，

在△中，因为，，

所以所以

（2）解：由（1）知。

因为，所以，

因为△的面积，

所以，，

由余弦定理

所以，

知识点

任意角的概念

题型：简答题

简答题 · 12 分

在ABC中，角A、B、C依次成等差数列，其对边依次分别为.

（1）若cos(B+C)= ，求cosC的值；

（2）若a＝3，·＝3，求b.

正确答案

（1）（2）7

解析

（1）在△ABC中，因为角A、B、C依次成等差数列，所以2B=A+C

又A+B+C=180°，所以B =60°………………………………………2分

由cos(B＋C)＝－，得sin(B＋C)＝＝ ……………3分

∴cosC＝cos[(B＋C)－B]＝cos(B＋C) cosB＋sin(B＋C) sinB

＝，…………………………………………6分

（2）由·＝3，得||·||cos(180°－C)＝3，即abcosC＝－3，

又a＝3，∴bcosC＝－1， ①……………………8分

由正弦定理＝，得＝，

∴bcosC＋bsinC＝3， ②……………………10分

将①代入②，得bsinC＝4， ③

将①②结合可得b＝7，………………………………12分

知识点

任意角的概念

题型：简答题

简答题 · 10 分

如图，ABC是⊙O 的内接三角形，PA是⊙O的切线，切点为A，PB交AC于点E，交⊙O于点D，PA=PE,∠ABC=45°，PD=1，DB=8.

（1）求ABP的面积；

（2）求弦AC的长。

正确答案

（1）（2）

解析

解析：（1）因为PA是的切线，切点为A，

所以，……………………1分

又PA=PE,所以45°，90°……2分

因为PD=1，DB=8，所以由切割线定理有，所以EP=PA=3，………………4分

所以△ABP的面积为BP·PA= ……………………5分

（2）在Rt△APE中，由勾股定理得 ……………………6分

又ED=EPPD=2，EB=DBDE=82=6，

所以由相交弦定理得 ……………………9分

所以EC，故AC= ………………………………10分

知识点

任意角的概念

题型：简答题

简答题 · 12 分

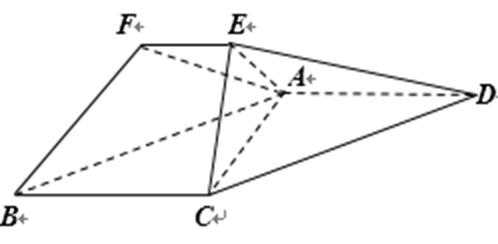
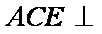
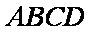
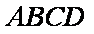
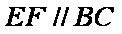
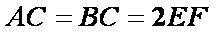
在如图所示的几何体中，平面平面，四边形为平行四边形，，，，。

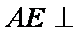
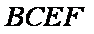
（1）求证：平面；

（2）求二面角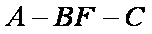的大小。

正确答案

见解析。

解析

（1）∵平面平面,且平面平面

平面 2分, ……3分

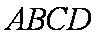
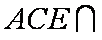
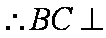
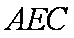
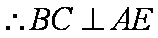
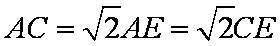
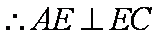
又, …………………4分

且,∴平面. …………………6分

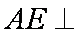
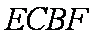
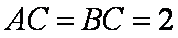
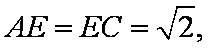
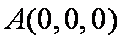
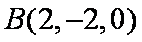
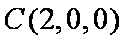
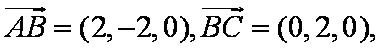
（2）（解法一）建立如图空间直角坐标系不妨设，则则由题意得，,,……8分

设平面的法向量为，由,得………9分设平面的法向量为，由，得………10分

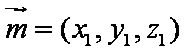
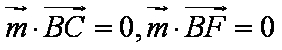
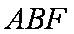
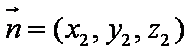
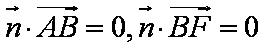
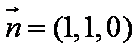
所以∴二面角的大小为 ………………12分

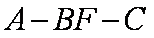
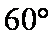
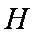
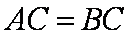
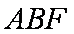
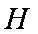
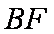
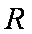
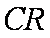
（解法二）取的中点，连接，因为，则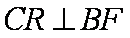，∴平面(要证明)，过向引垂线交于，连接，

则，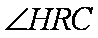

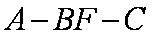
则为二面角的平面角. ……9分

由题意，不妨设，

连接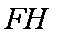，则，又

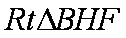
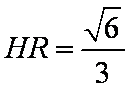
因此在中，,,

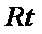
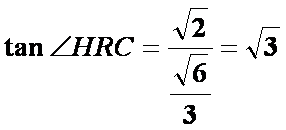
所以在△CHR中， …………11分

因此二面角的大小为 …………12分

知识点

任意角的概念

继续学习学习下一知识点

下一知识点 : 终边相同的角

百度题库 > 高考 > 理科数学 > 任意角的概念

扫码查看完整答案与解析