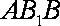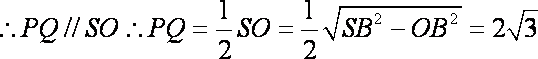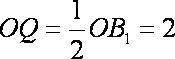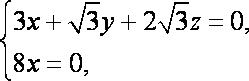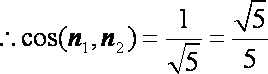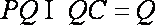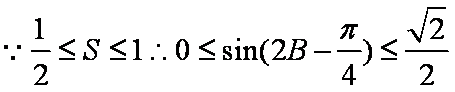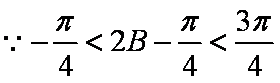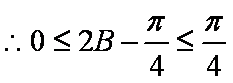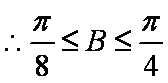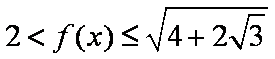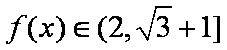- 任意角的概念
- 共691题
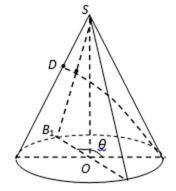
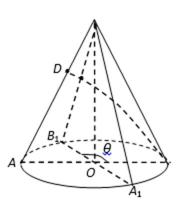
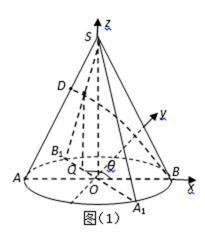
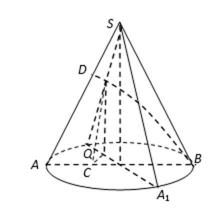
如图已知圆锥
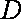
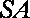
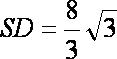
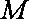
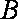
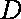
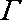
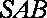
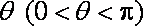
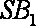
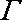
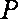
(1)若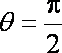
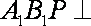
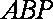
(2)若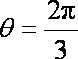
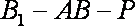
正确答案
见解析
解析
本小题主要考查直线与平面的位置关系,二面角的大小等基础知识,考查空间想象能力、推理论证能力和运算求解能力,考查化归与转化思想、数形结合思想。
解法一:(1)证明:∵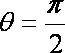
∴
∵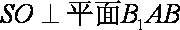

又∵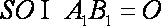
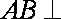
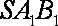
又∵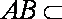
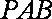
∴平面
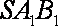
又∵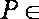
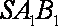
∴平面
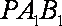
(2)以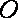
OS所在直线为z轴建立如图(1)所示的空间直角坐标系,…………8分
则
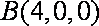
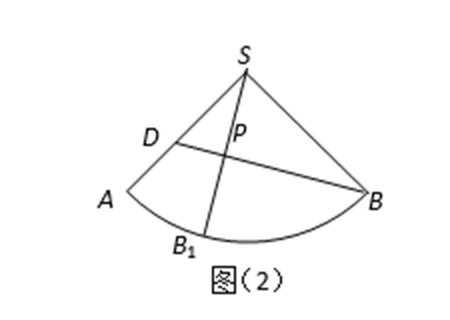
将圆锥半侧面图展开,如图(2)所示,
由已知可求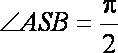
又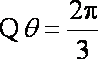
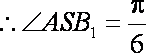
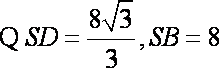
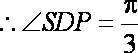
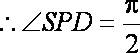
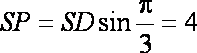
∴点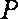
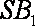
如图(1)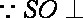
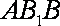
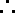
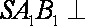
过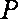
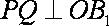
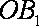
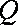
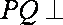
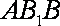
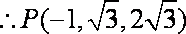
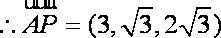
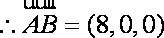
设平面
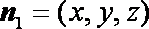
解得: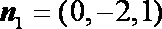
取平面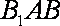
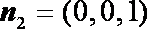
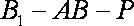
解法二:(1)同解法一;
(2)与解法一同,得: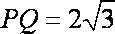
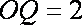
过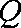
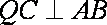
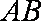
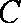
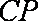
∵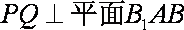
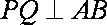
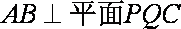

则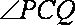
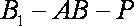
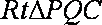
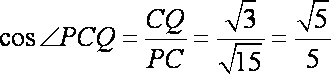
知识点
已知

正确答案
答案:
解析

知识点
在△ABC中,角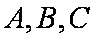
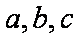
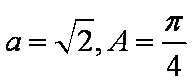
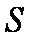
(1)若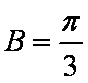
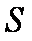
(2)若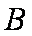
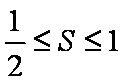
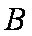
正确答案
见解析
解析
(1)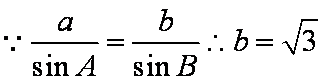
(2)
知识点
在三角形

(1)求角
(2)若


正确答案
(1)
解析
(1) 由题
则

即


从而

(2) 由

所以

当



当

所以由

所以
综上可知
知识点
已知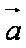
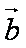
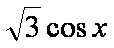
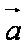
(1)求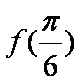
(2)当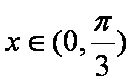
正确答案
见解析
解析
(1)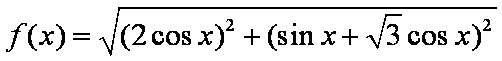
∴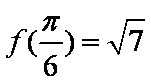
(2)∵ 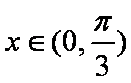
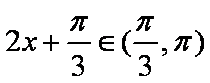
∴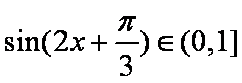
∴
∴
知识点
如图,在



(1)求
(2)设



正确答案
见解析
解析
(1)由已知得
则
又

(2)设

由已知得

故

则
由余弦定理得
知识点
已知函数
(1)求
(2)求函数
正确答案
见解析
解析
(1)
(2)



因为

所以

因为函数

由
得
所以

知识点
设函数


(1)若曲线




(2)若

①求证:


正确答案
见解析
解析
(1)
依据题意得:




如图,得
∴

代入


(2)①

②

若


所以



若

又
所以



若


所以



综上知

知识点
在






正确答案
解析
由












知识点
已知



(1)求角
(2)求函数
正确答案
见解析
解析
(1)由正弦定理,得:
即
故
所以
(2)
所以所求函数值域为
知识点
扫码查看完整答案与解析