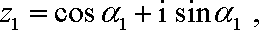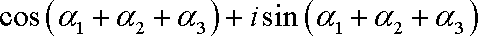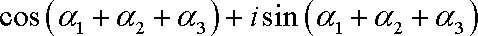- 任意角的概念
- 共691题
在△ABC中,已知AB=2,AC=
(1)求角B的值;
(2)若四边形ACDE的面积为
正确答案
(1)
(2)9
解析
(1)由余弦定理得:
所以B=
(2)设AE=x,CD=y则
∵
∴
∴
∴
∴

所以AE·CD的最大值为9
知识点
设







(1)当


正确答案
见解析。
解析
(1)因为

因为



因为


(2)因为

所以当

因为

因为

所以

所以

知识点
小明在做一道数学题目时发现:若复数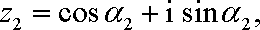
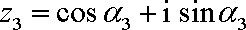
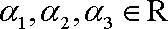
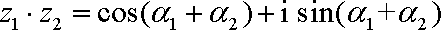
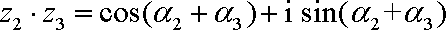
正确答案
解析
运用推理
知识点
已知在锐角△ABC中,角A、B、C所对的边分别为



(1)求角C的大小;
(2)当

正确答案
见解析。
解析
(1)由

结合余弦定理得:
(2)由正弦定理得:
∴
∴
∵△ABC是锐角三角形,由


知识点
在△ABC中,

(1)求
(2)设
正确答案
见解析。
解析
(1)在

又∵

(2)由正弦定理知:

知识点
已知函数
(1)求
(2)若对任意


(3)设






正确答案
见解析。
解析
(1)∵
∴当




当


(2)由

∵

∵对任意

∴



令

∵
∴



(3)由条件,
假设曲线






不妨设

∴

是否存在

①若



②若



若a>0时,有
设

显然, 当









综上所述,曲线




知识点
已知函数

(1)求实数
(2)在锐角



正确答案
见解析
解析
(1)由已知可得:
=3cosωx+
因为函数f(x) 图像相邻两对称中心之间的距离为
.所以

(2)因为


所以


=
在锐角


知识点
已知三棱柱






(1)求证:

(2)求二面角
正确答案
见解析。
解析
(1)连接


△




∴ 



∴ 

(2)建系
由题可知:
设平面







故二面角

知识点
己知函数
(1)当

(2)设








正确答案
见解析 。
解析
(1)
∵

∴
则

(2)

∵



∵向量



由余弦定理得,

由①②解得
知识点
若斜率为

















(1)若点P横坐标为0,求
(2)试判断



(3)求证:函数
正确答案
见解析。
解析
(1)由






(2)


由(1)知




在函数

当





当







同理可证

对任意x∈R,




(3)证明:设





即








知识点
扫码查看完整答案与解析