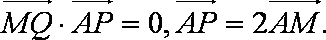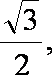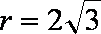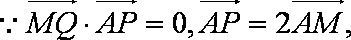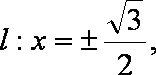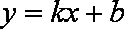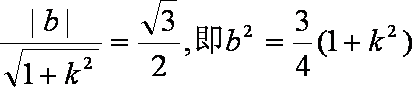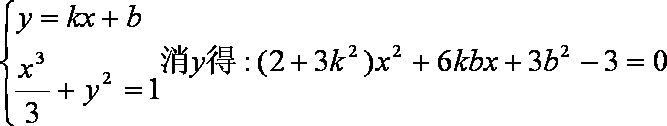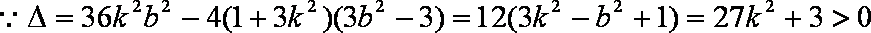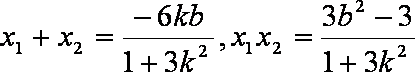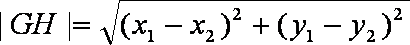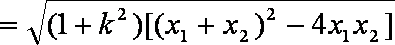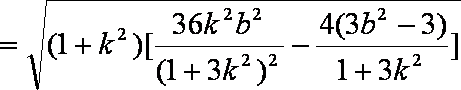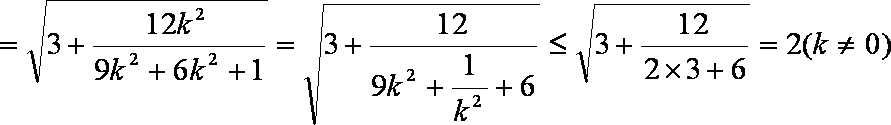- 任意角的概念
- 共691题
在




(1)若


(2)若

正确答案
见解析。
解析
(1)由余弦定理及已知条件得,
又因为



联立方程组


(2)由题意得
即
当




当


联立方程组


所以

知识点
在△




(1)求内角
(2)若

正确答案
(1)
(2)
解析
(1)∵

∴


∴

∵

(2)∵

∵

∵
∴当且仅当

知识点
如图一,△ABC是正三角形,△ABD是等腰直角三角形,AB=BD=2。将△ABD沿边AB折起, 使得△ABD与△ABC成30o的二面角

(1) 求D、C之间的距离;
(2) 求CD与面ABC所成的角的大小;
(3)求证:对于AD上任意点H,CH不与面ABD垂直。
正确答案
见解析。
解析
依题意,





(1)|CD|=
(2)
设CD与面ABC成的角为







(3) 设










若


此时


而









即CH不可能同时垂直BD和BA,即CH不与面ABD垂直。
知识点
已知C为圆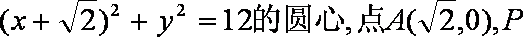
(1)当点P在圆上运动时,求点Q的轨迹E的方程;
(2)一直线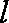
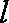
(a)求证直线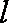
(b)若直线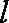
求△OGH的面积的最大值。
正确答案
见解析。
解析
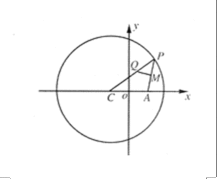
(1)圆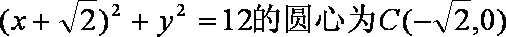
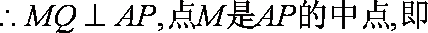
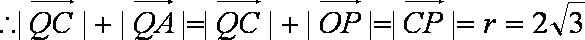
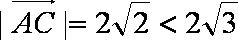
根据椭圆的定义,点Q轨迹是以C(-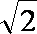
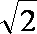
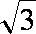
由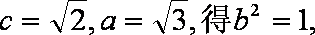
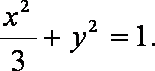
(2)(a)证明:当直线l垂直x轴时,由题意知:
不妨取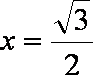
即G(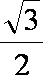
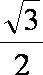
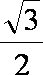
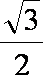
当直线l不垂直x轴时,设直线l的方程为:
由题意知:
由
∴直线l与椭圆E交于两点
综上,直线l必与椭圆E交于两点…………………………8分
(b)由(a)知当直线l垂直x轴时,
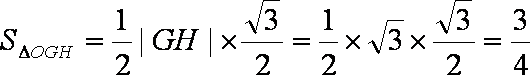
当直线l不垂直x轴时
设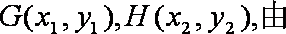
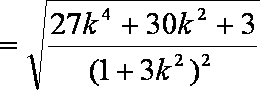
当且仅当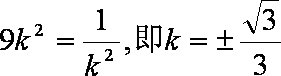
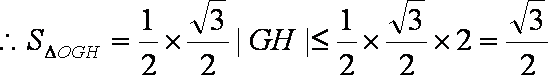
当k=0时,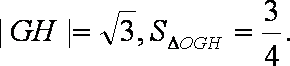
综上,△OGH的面积的最小值为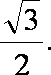
知识点
在极坐标系



正确答案
解析
直线



知识点
扫码查看完整答案与解析