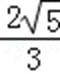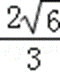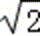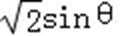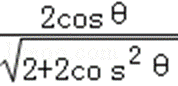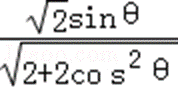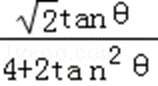任意角的概念
共691题

· 任意角的概念

任意角的概念
共691题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 14 分

17.已知数列{an}前n项和为Sn，满足2Sn+ n2 = 3an-6,(n∈N*)

（1）求数列{an}的通项公式；

（2）求证：，(n≥2，n∈N*)

（3）设 ,(n≥2，n∈N*),求证：

正确答案

见解析。

解析

（1）由①得,当n=1时，=7，

当时，②,

①－②得

，()

∴，()

又+2=9，所以数列是首项为9公比为3的等比数列.

，∴

（2）由(1)可知＝＝

易知时，，∴

()

（3）＝，（）

令，（x≥２）

在[２，＋∞）上恒成立，

所以在[２，＋∞）上单调递减，

∴，

令则得

即，

∴（）.

故

知识点

任意角的概念

题型：单选题

单选题 · 5 分

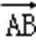
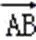
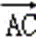
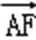
10.在△ABC中，若|+|=|﹣|，AB=2，AC=1，E，F为BC边的三等分点，则•=（　　）

A．

B．

C．

D．

正确答案

解析

若|+|=|﹣|，

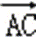
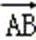
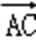
则=，

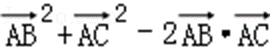
即有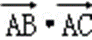=0，

E，F为BC边的三等分点，

则=（+）•（+）=（）•（）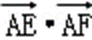

=（+）•（+）

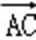
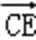
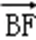
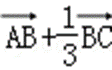
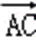
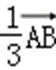
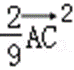
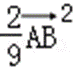
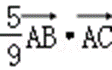
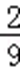
=++=×（1+4）+0=．

故选B．

知识点

任意角的概念

题型：单选题

单选题 · 5 分

3.由y=f（x）的图象向左平移个单位，再把所得图象上所有点的横坐标伸长到原来的2倍得到y=2sin的图象，则 f（x）为（　　）

A2sin

B2sin

C2sin

D2sin

正确答案

解析

略。

知识点

任意角的概念

题型：简答题

简答题 · 7 分

16.已知在中，角所对的边分别为，，且为钝角。

（1）求角的大小；

（2）若，求的取值范围。

正确答案

见解析。

解析

（1）由得，得

于是又，∴

（2）∵为钝角，于是，又，∴

由正弦定理可知，

又，

∴

知识点

任意角的概念

题型：简答题

简答题 · 13 分

17.如图三棱柱中，侧面为菱形，。

（1）证明：；

（2）若，，AB=BC，求二面角的余弦值。

正确答案

见解析。

解析

（1）连结，交于O，连结AO，因为侧面为菱形，所以，且O为与的中点，又，所以平面，故又，故

（2）因为且O为的中点，所以AO=CO因为AB=BC，所以

故OA⊥OB，从而OA，OB，两两互相垂直，

以O为坐标原点，OB的方向为x轴正方向，OB为单位长，建立如图所示空间直角坐标系O-，因为，所以为等边三角形，又AB=BC，则

，，，

，

设是平面的法向量，则

，即所以可取

设是平面的法向量，则，同理可取

则，所以二面角的余弦值为.

知识点

任意角的概念

题型：单选题

单选题 · 5 分

11.已知正三棱柱ABC－A1B1C1的侧棱长与底面边长相等，则AB1与侧面ACC1A1所成角的正弦值等于(　　)

C‍

D‍

正确答案

解析

如图，以A1C1中点E为原点建立空间直角坐标系E－xyz，设棱长为1，则A，B1，设AB1与平面ACC1A1所成的角为θ，EB1为平面ACC1A1的法向量．

则sinθ＝|cos〈，〉|＝＝.

知识点

任意角的概念

题型：简答题

简答题 · 12 分

17.在△ABC中，角A，B，C的对边分别为a，b，c，且满足（2c－ a）cosB－ bcos A=0。

（1）求角B的大小

（2）求的取值范围

正确答案

（1）

（2）

解析

（1）即

（2）由（1）知,

的取值范围

知识点

任意角的概念

题型：简答题

简答题 · 14 分

19.已知正项数列{}的前n项和为，对∈N﹡有＝。

（1）求数列{}的通项公式；。

（2）令，设{}的前n项和为，求T1，T2，T3，…，T100中有理数的个数。

正确答案

见解析。

解析

（1）当时或0（舍去）

当时

两式相减得，

所以数列是以1为首项，1为公差的等差数列）

（2）

在有理数中有共9个。

知识点

任意角的概念

题型：单选题

单选题 · 5 分

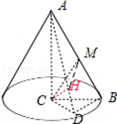
9.等腰Rt△ACB，AB=2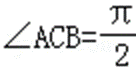，，以直线AC为轴旋转一周得到一个圆锥，D为圆锥底面一点，BD⊥CD，CH⊥AD于点H，M为AB中点，则当三棱锥C﹣HAM的体积最大时，CD的长为（　　）

正确答案

解析

根据题意，得

∵AC⊥平面BCD，BD⊂平面BCD，∴AC⊥BD，

∵CD⊥BD，AC∩CD=C，∴BD⊥平面ACD，可得BD⊥CH，

∵CH⊥AD，AD∩BD=D，∴CH⊥平面ABD，可得CH⊥AB，

∵CM⊥AB，CH∩CM=C，∴AB⊥平面CMH，

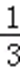
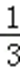
因此，三棱锥C﹣HAM的体积V=S△CMH×AM=S△CMH由此可得，当S△CMH达到最大值时，三棱锥C﹣HAM的体积最大

设∠BCD=θ，则Rt△BCD中，BC=AB=

可得CD=，BD=

Rt△ACD中，根据等积转换得CH==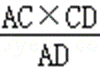

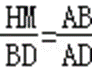
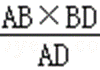
Rt△ABD∽Rt△AHM，得，所以HM==

因此，S△CMH=CH•HM==

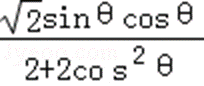
∵4+2tan2θ≥4tanθ，

∴S△CMH=≤=，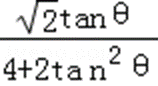

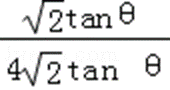
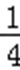
当且仅当tanθ=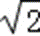时，S△CMH达到最大值，三棱锥C﹣HAM的体积同时达到最大值。

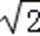
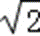
∵tanθ=＞0，可得sinθ=cosθ＞0

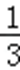
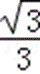
∴结合sin2θ+cos2θ=1，解出cos2θ=，可得cosθ=（舍负）

由此可得CD==，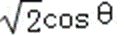

即当三棱锥C﹣HAM的体积最大时，CD的长为，故选C。

知识点

任意角的概念

题型：填空题

填空题 · 4 分

14.如图，中，，，点在边上，，则的长度等于（）

正确答案

解析

由余弦定理,所以.

再由正弦定理，即，所以。

知识点

任意角的概念

继续学习学习下一知识点

下一知识点 : 终边相同的角

百度题库 > 高考 > 理科数学 > 任意角的概念

扫码查看完整答案与解析