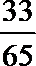任意角的概念
共691题

· 任意角的概念

任意角的概念
共691题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 12 分

16．若的图像与直线相切，并且切点横坐标依次成公差为的等差数列.

（1）求和的值；

（2）在⊿ABC中，a、b、c分别是∠A、∠B、∠C的对边。若是函数图象的一个对称中心，且a=4，求⊿ABC外接圆的面积。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

任意角的概念

题型：单选题

单选题 · 6 分

4.在平面直角坐标系内，若曲线：上所有的点均在第二象限内，则实数的取值范围为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

任意角的概念

题型：填空题

填空题 · 5 分

10. 已知cos 31°＝m，则sin 239°·tan 149°的值是________

正确答案

解析

sin 239°·tan 149°＝sin (270°－31°)·tan (180°－31°)＝－cos 31°·(－tan 31°)＝cos 31°·tan 31°＝sin 31°＝

知识点

任意角的概念

题型：简答题

简答题 · 14 分

18.如图，已知△ABC内接于圆O，AB是圆O的直径，四边形DCBE为平行四边形，DC⊥平面ABC,AB=2,tan∠EAB=

（1）证明：平面ACD⊥平面ADE;

（2）当 AC=x时， V(x)表示三棱锥A-CBE的体积，当V(x)取得最大值时，求直线AD与平面ACE所成角的正弦值。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

任意角的概念

题型：单选题

单选题 · 5 分

7.将函数的图像向右平移单位得到函数的图像，则将函的横坐标伸长到原来的2倍，纵坐标不变，得到函数的图像，则（）

A‍‍

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

任意角的概念

题型：单选题

单选题 · 5 分

6．定义行列式运算：将函数的图象向左平移m个单位，所得图像对应的函数为偶函数，则m的最小值是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

任意角的概念

题型：填空题

填空题 · 5 分

9.已知_________。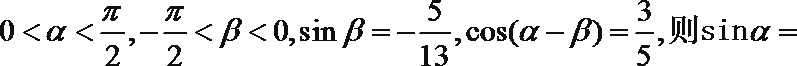

正确答案

解析

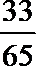
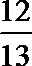
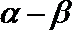
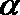
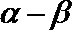
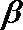
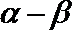
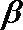
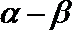
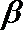
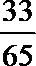
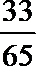
由题意得cos=,sin()=,则sin=sin(+)=sin()cos+cos()sin=,故答案为。

知识点

任意角的概念

题型：简答题

简答题 · 13 分

18．如图,游客从某旅游景区的景点处下山至处有两种路径.一种是从沿直线步行到,另一种是先从沿索道乘缆车到,然后从沿直线步行到.现有甲、乙两位游客从处下山,甲沿匀速步行,速度为.在甲出发后,乙从乘缆车到,在处停留后,再从匀速步行到.假设缆车匀速直线运动的速度为,山路长为,经测量,,.

（Ⅰ）问乙出发多少分钟后,乙在缆车上与甲的距离最短?

（Ⅱ）为使两位游客在处互相等待的时间不超过分钟,乙步行的速度应控制在什么范围内?

正确答案

解: （Ⅰ）∵,∴∴,

∴

根据得,

所以乙在缆车上的时间为（min）.

设乙出发（）分钟后,甲、乙距离为,

则

∴时,即乙出发分钟后,乙在缆车上与甲的距离最短.

（Ⅱ）由正弦定理得(m).

乙从出发时,甲已经走了50(2+8+1)=550(m),还需走710m才能到达.

设乙步行速度为,

则.解得.

∴为使两位游客在处互相等待的时间不超过分钟,乙步行的速度应控制在范围内.

解析

解析已在路上飞奔，马上就到！

知识点

任意角的概念

题型：简答题

简答题 · 14 分

19．已知向量，设函数,若函数的图象与的图象关于坐标原点对称.

（Ⅰ）求函数在区间上的最大值,并求出此时的值；

（Ⅱ）在中，分别是角的对边，为锐角,若，，的面积为，求边的长．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

任意角的概念

题型：简答题

简答题 · 12 分

16．在中，已知，

（1）求的值；

（2）若，求的面积；

（3）若函数，求的值。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

任意角的概念

继续学习学习下一知识点

下一知识点 : 终边相同的角

百度题库 > 高考 > 理科数学 > 任意角的概念

扫码查看完整答案与解析