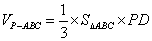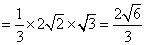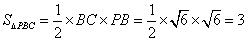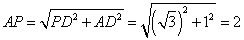- 任意角的概念
- 共691题
已知函数
(1)求
(2)设


正确答案
见解析
解析
(1)解:

(2)解:因为
所以

因为
因为

所以

知识点
已知函数
(1)求f(x)的最值;
(2)求f(x)的单调增区间。
正确答案
见解析。
解析
解:(1)
=
=
f(x)的最大值为1、最小值为0;
(2)f(x)单调增,故
从而f(x)的单调增区间为
知识点
在








(1)求证:
(2)如图6,设圆



正确答案
见解析
解析
(1)证明:由正弦定理得



又因为






由


(2)由(1)及








因为




知识点
在



(1)求
(2)求
正确答案
见解析
解析
(1)由正弦定理


(2)由余弦定理,得
所以
故
所以
知识点
已知△





(1)求
(2)求
(3)求向量

正确答案
见解析。
解析
(1)由
得
∵
(2)由(1)得
∵
∴
∴
∴
(3)∵
设向量


∴
知识点
记直线




正确答案
解析
略
知识点
在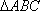

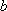

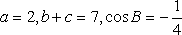
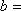
正确答案
4
解析
略
知识点
(1)求角C的大小;
(2)求
正确答案
见解析。
解析
(1)由
即
(2)由(1)得

∴当

知识点
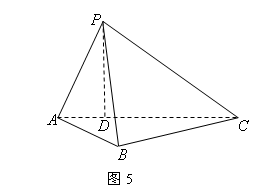
如图5所示,在三棱锥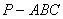
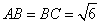
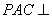
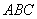
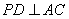
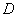
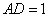
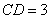
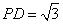
(1)证明△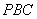
(2)求直线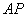
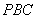
正确答案
见解析
解析
解析:(1)证明略
(2)过点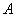
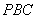
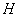
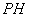
则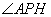
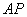
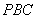
由(1)知,△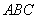
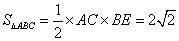
因为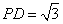
由(1)知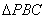
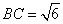
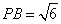
所以△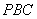
因为三棱锥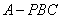
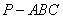

即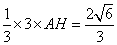
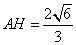
在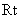
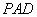
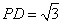
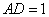
所以
因为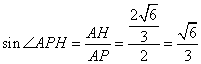
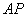
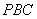
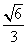
知识点
已知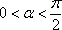

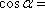
正确答案
解析
知识点
扫码查看完整答案与解析