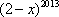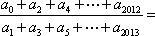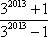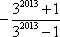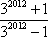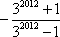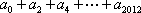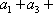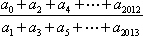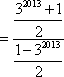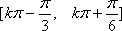- 任意角的概念
- 共691题
1
题型:简答题
|
已知△ABC的三个内角A、B、C所对的边分别为


(1)求cosC的值;
(2)当

正确答案
见解析。
解析
(1)在△ABC中,因为

又

所以


所以
(2)由(1)知
所以

又

知识点
任意角的概念
1
题型:
单选题
|
若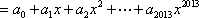
正确答案
B
解析
令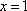
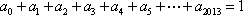
令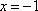
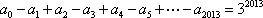
由①②联立,可得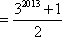
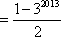
从而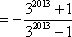
知识点
任意角的概念
1
题型:简答题
|
在△ABC中,三个内角分别为A,B,C,已知

(1)求cosC的值;
(2)若BC=10,D为AB的中点,求CD的长。
正确答案
见解析。
解析
(1)因为


则

(2)由(1)可得
由正弦定理得

因为在△BCD中,

所以
知识点
任意角的概念
1
题型:简答题
|
已知函数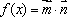
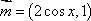
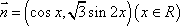
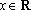
(1)求
(2)在△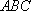

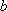

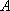
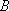
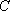
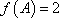
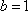
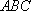
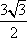

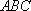
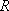
正确答案
见解析
解析
(1)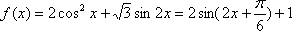
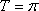
单调递增区间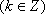
(2)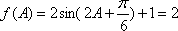
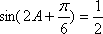
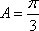
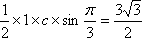
∴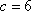
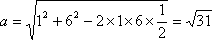
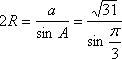
∴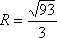
知识点
任意角的概念
1
题型:简答题
|
在平面直角坐标系




(1)求
(2) 求
正确答案
见解析。
解析
本小题考查三角函数的定义、两角和的正切、二倍角的正切公式。
(1)由条件得 





因此

(2)




且

同理

从而
知识点
任意角的概念
下一知识点 : 终边相同的角
扫码查看完整答案与解析