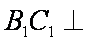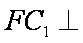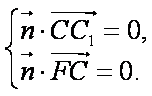- 任意角的概念
- 共691题


正确答案
解析
由程序框图知,



知识点
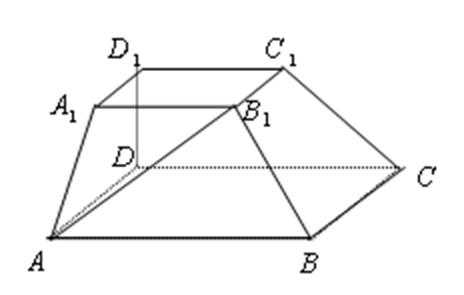
如图1,





(1)证明:
(2)设






(3)设







正确答案
见解析
解析
(1)∵











(2)由(1)


又
∴
(3)连接





∵



而



∴

即在线段



此时
知识点
如图,某观测站C在城A的南偏西

正确答案
见解析。
解析
在


所以




所以
由正弦定理 
所以
故这时此车距离A城15千米………………………………………………………12分
知识点
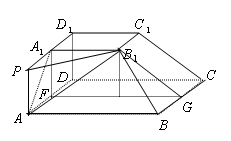
如图,在多面体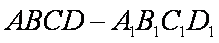
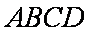
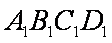
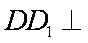
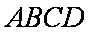
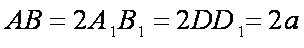
(1)求异面直线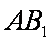
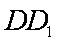
(2)试在平面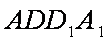
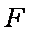
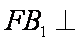
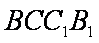
(3)在(2)条件下,求二面角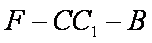
正确答案
见解析
解析
解法1:
(1)过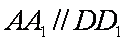
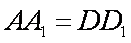
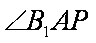
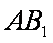
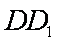
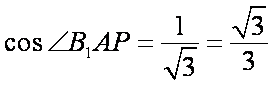
(2)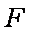
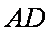
∵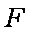
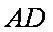
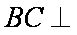
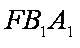
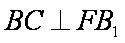
∵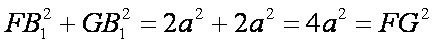
∴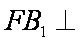
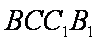
(3)由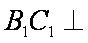
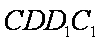
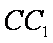
又由(2)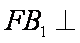
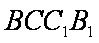
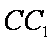
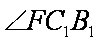
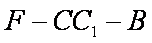
∵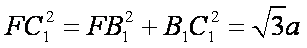
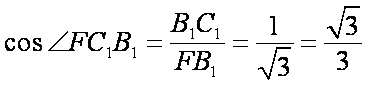
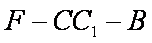
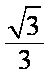
解法2:以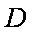
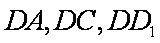
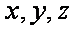
(1)∵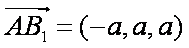

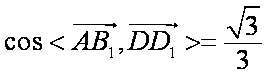
(2)设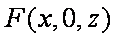
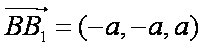
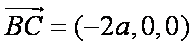
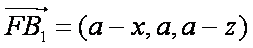
……6分
由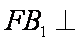
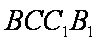
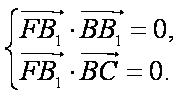
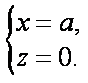
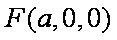
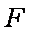
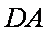
…………7分
(3)由(2)知,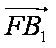
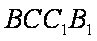
设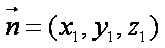
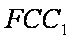

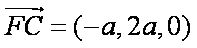
由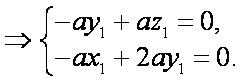
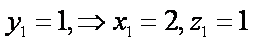
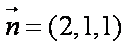
∴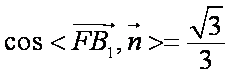
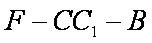
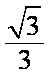
知识点
如图,已知O为


(1)证明:
(2)求
正确答案
见解析
解析
(1)取AB、AC的中点E、F,
则
同理
所以
(2)
知识点
扫码查看完整答案与解析