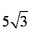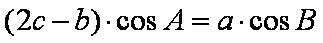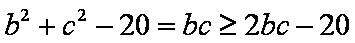- 任意角的概念
- 共691题
在△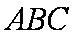
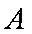
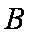

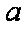
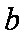
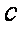
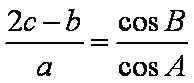
(1)求角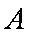
(2)若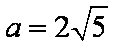
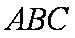
正确答案
(1)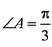
解析
(1)因为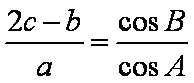
所以
由正弦定理,得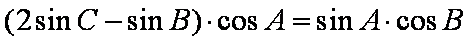
整理得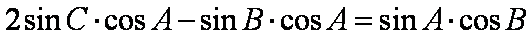
所以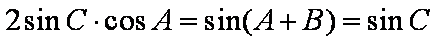
在△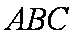
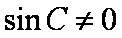
所以
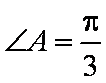
(2)由余弦定理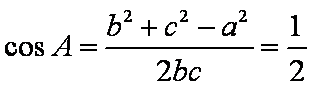
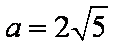
所以
所以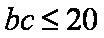
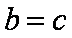
所以三角形的面积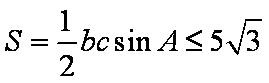
所以三角形面积的最大值为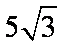
知识点
已知


正确答案
解析
因为

知识点
设r>0,那么直线



正确答案
解析
圆


知识点
四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC



(1)证明:SA
(2)求直线SD与平面SAB所成角的正弦值。
正确答案
见解析
解析
(1)作


由侧面

得

因为

又


如图,以












(2)设
则

令x=1 





所以,直线


知识点
在△ABC中,若a=2,∠B=60°,b=
正确答案
解析
∵△ABC中,a=2,b=
∴根据余弦定理,得b2=a2+c2﹣2accosB,
可得7=4+c2﹣4ccos60°,化简得c2﹣2c﹣3=0,解之得c=3(舍负)
∴△ABC的面积S=

又∵△ABC的面积S=
∴h=

知识点
扫码查看完整答案与解析