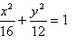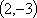- 定义法求轨迹方程
- 共148题
若



正确答案
1
解析
当 
知识点
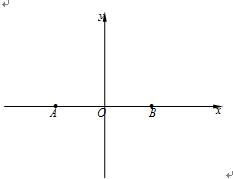
在直角坐标系








(1)求动点

(2)设曲线







(3)若直线





正确答案
见解析
解析
解:(1)由已知,得
将两边平方,并化简得


(2)由已知可得


因为

即得
故线段


因为




将④代入②,并令



所以



因为


将(1)代入(2)得
由于直线

从而可得

同理,由




由(3)、(4)得



即





知识点
在极坐标系中,曲线


正确答案
解析
解析1:由

解析2:由


知识点
某海域有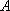
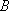
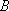
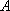
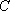
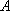
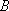
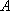
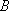

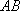
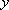
(1)求曲线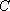
(2)某日,研究人员在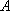
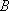
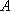
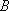
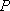
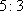
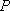
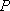
正确答案
(1)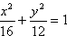
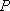
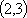
解析
解析:(1)由题意知曲线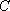
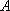
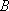
又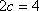
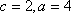
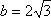
所以曲线
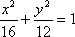
(2)由于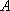
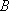
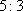
因此设此时距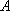
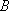
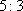
即鱼群分别距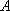
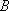
设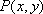
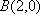
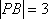
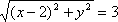
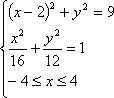
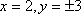


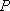
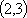
知识点
已知椭圆










(1)求曲线
(2)设




(3)设






正确答案
见解析
解析
解析:(1)解双曲线

(2)设点







则直线

联立方程组
整理,得



同理可得,

(3)解:设点




则

因为


因为点



因为点

因为

所以
由(2)知,




设

当



所以函数


因为

所以当


当


所以

知识点
扫码查看完整答案与解析