- 定义法求轨迹方程
- 共148题
已知F1(-1,0),F2(1,0)为平面内的两个定点,该平面内的动点P满足
|PF1|+|PF2|=2
(1)求曲线E的方程;
(2)设点O为坐标原点,A,B,C是曲线E上的不同三点,且
(i)证明:直线AB与OC的斜率之积为定值;
(i i)当直线AB过点F1时,求直线AB、OC与x轴所围成的三角形的面积。
正确答案
见解析。
解析
(1)由条件可知, 点


所以点





(2)设


由


(ⅰ)可设直线

代入

依题意,


从而可得点


因为


(ⅱ)若


得点



由(ⅰ)可知,当直线




代入


所以
(1)当


故





(2)当


同理可求直线



综合(1)(2),直线



知识点
动圆




(1)求曲线C的方程;
(2)过点











正确答案
见解析
解析
(1)点








(2)设直线



由

∴
设
由

∴
∴

∴

知识点
在极坐标系中, 




正确答案
见解析
解析
圆的方程可化为

又直线方程可化为
所以圆心到直线的距离
知识点
已知曲线

正确答案
解析
设切点的横坐标为(x0,y0)
∵曲线

∴y′=


知识点
在平面直角坐标系下,曲线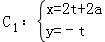
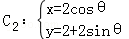
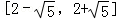
正确答案
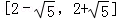
解析
曲线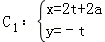
曲线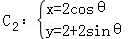
由曲线Cl、C2 有公共点,可得圆心到直线的距离小于或等于半径,∴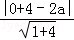
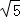
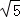
知识点
扫码查看完整答案与解析









