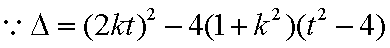- 定义法求轨迹方程
- 共148题
选修4-4:坐标系与参数方程
在极坐标系中,过点

(1)将

(2)在极坐标系中,以极点为坐标原点,以极轴为
若曲线






正确答案
见解析。
解析
(1)画图可知
(2)直线



知识点
在直角坐标平面内,将每个点绕原点按逆时针方向旋转





(1)求矩阵

(2)求曲线


正确答案
(1)
解析
(1)在直角坐标平面内,将每个点绕原点按逆时针方向旋转


(2)将每个点横、纵坐标分别变为原来的







(1)


(2)




故所求的曲线方程为:
知识点
在直角坐标平面内,以坐标原点






(1)分别求出曲线

(2)若点




正确答案
(1)

解析
(1)由曲线






(2)由圆心(2,0)到直线




(1)由







即
(2)因为圆心







知识点
选修4-2:矩阵与变换
若点




(2)求曲线C:x2+y2=1在矩阵N=
正确答案
见解析。
解析
法一:



即M=




法二:同法一可求得M=






(2)
知识点
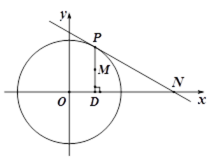
如图,在圆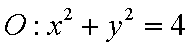
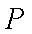
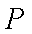
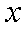
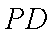
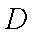
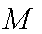
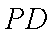
(1)当点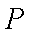

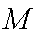
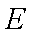
(2)若圆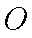
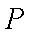
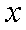


正确答案
(1)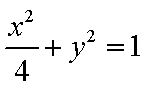
解析
(1)由于点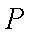

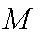
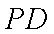
(2)由(1)得到轨迹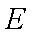


(1)设
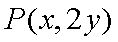

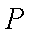


即点
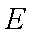

(2)解法一:
(i) 当直线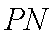


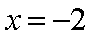
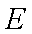
(2)当直线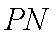

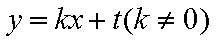
因为直线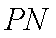

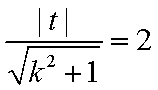
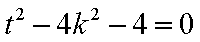
又直线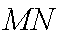
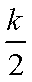
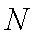
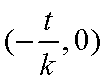
所以直线
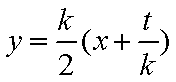
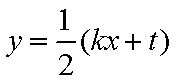
由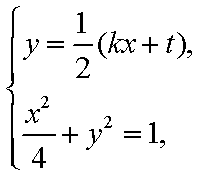
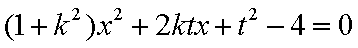
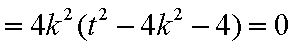

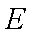
综上(i)(2)知,直线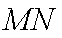
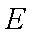
解法二 :设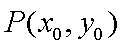

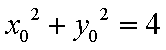
(i)当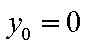


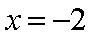


(2)当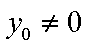

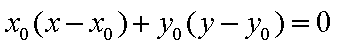
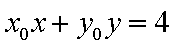
令
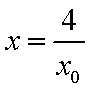
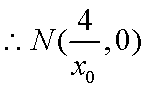
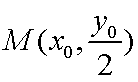
所以直线
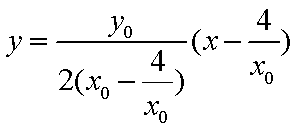

由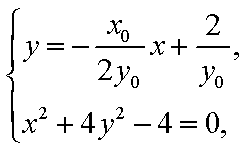

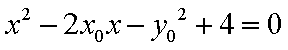
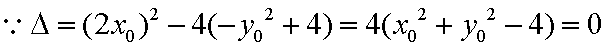
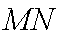

综上(i)(2)知,直线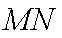

知识点
扫码查看完整答案与解析