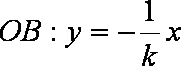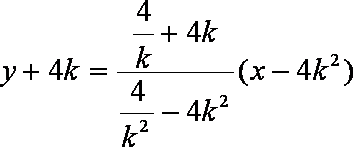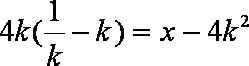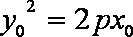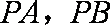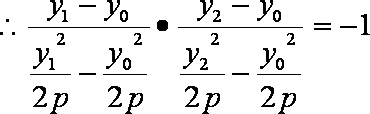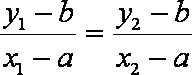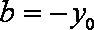- 定义法求轨迹方程
- 共148题
11.已知曲线

正确答案

解析
分焦点在x轴和y轴上两种情况,
当焦点在x轴上时,

当焦点在y轴上时,

知识点
选修4—4:极坐标与参数方程
在直角坐标平面内,以坐标原点






(1)分别求出曲线

(2)若点




正确答案
见解析。
解析
(1)由







即
(2)因为圆心







知识点
已知动点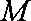
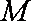
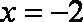
(1)求点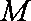
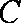
(2)大家知道,过圆上任意一点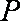
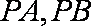
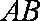
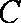
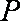
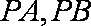
(ⅰ)若点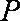
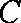
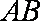
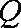
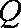
(ⅱ)试探究:若改变曲线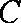
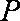
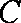
正确答案
见解析。
解析
(1)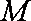
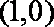
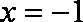
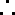
轨迹方程为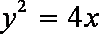
(2)(i)依题意得设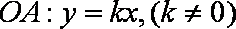
由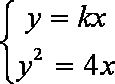
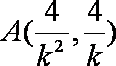
同理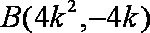
因此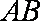
即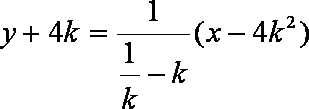
令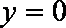
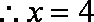
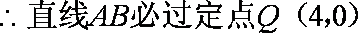
(ii)结论:过抛物线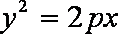
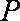
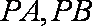
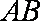
设点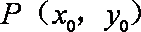
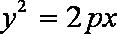
过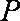
设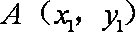
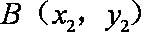
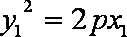
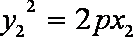
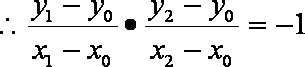
化简得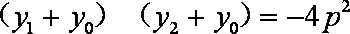
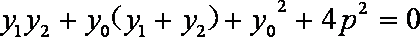
假设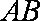
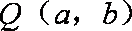
即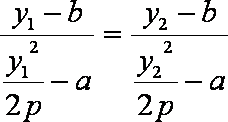
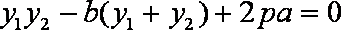
比较(*)、(**)得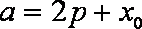
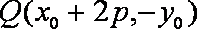
(如用其它方法,请对照给分)
知识点
已知





(1)求点P的轨迹方程;
(2)是否存在定直线

正确答案
见解析。
解析
(1)设B(0,t),设Q(m,0),t2=


















(2)由(1),点P的轨迹方程是y2=x;设P(y2,y),


L=2
=2

若a为常数,则对于任意实数y,L为定值的条件是a-





知识点
20.已知动圆












(1)求曲线
(2)试探究

(3)记





正确答案
见解析。
解析
(1)设圆心

由于动圆


圆





故圆心

(2)设

由

由


(3)




令







知识点
扫码查看完整答案与解析