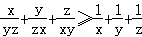- 不等式的证明
- 共16题
已知x,y,z均为正数,求证: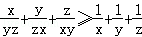
正确答案
见解析。
解析
因为x,y,z都是为正数,
所以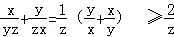
同理可得
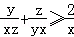
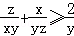
当且仅当x=y=z时,以上三式等号都成立。
将上述三个不等式两边分别相加,并除以2,
得:
知识点
已知

正确答案
见解析
解析
证明:由柯西不等式得
则
知识点
设a、b是非负实数,求证:
正确答案
见解析。
解析
(方法一)证明:
因为实数a、b≥0,
所以上式≥0。即有
(方法二)证明:由a、b是非负实数,作差得
当



当



所以
知识点
将一个正整数






(1)写出
(2)对任意正整数


(3)当正整数

正确答案
见解析
解析
(1)解:因为3=3,3=1+2,3=1+1+1,所以
因
所以
(2)结论是
证明如下:由结论知,只需证
因为









所以





同样,把一个








所以有
(3)由第(2)问可知:
当正整数

又

对于*式,分别取


即
知识点
已知函数
(1)解不等式
(2)若

正确答案
见解析
解析
(1)f(x)+f(x+4)=|x-1|+|x+3|=
当x<-3时,由-2x-2≥8,解得x≤-5;
当-3≤x≤1时,f(x)≤8不成立;
当x>1时,由2x+2≥8,解得x≥3. …4分
所以不等式f(x)≤4的解集为{x|x≤-5,或x≥3}, …5分
(2)f(ab)>|a|f(),即|ab-1|>|a-b|, …6分
因为|a|<1,|b|<1,所以|ab-1|2-|a-b|2
=(a2b2-2ab+1)-(a2-2ab+b2)
=(a2-1)(b2-1)>0,
所以|ab-1|>|a-b|,故所证不等式成立, 10分
知识点
扫码查看完整答案与解析