- 圆的方程
- 共331题
已知圆C方程:(x-1)2 + y 2=9,垂直于x轴的直线L与圆C相切于N点(N在圆心C的右侧),平面上有一动点P,若PQ⊥L,垂足为Q,且
(1)求点P的轨迹方程;
(2)已知D为点P的轨迹曲线上第一象限弧上一点,O为原点,A、B分别为点P的轨迹曲线与
正确答案
见解析。
解析
(1)设

则
因为

化简得
所以点
(2)依题意得,


设

则四边形

又因为
所以
所以四边形

当四边形


此时
知识点
已知半圆


(1)求动圆圆心
(2)是否存在斜率为


正确答案
见解析
解析
(1)设动圆圆心


①若两圆外切: 




②若两圆内切: 




综上,动圆圆心的轨迹方程是




其图象为两条抛物线位于
(2)假设直线


依题意得,它与曲线



即







即




将其代入方程①得 
因为曲线


知识点
如图,





求证:
正确答案
见解析。
解析
因为



所以
故直角三角形

则

知识点
如图,AB是半圆O的直径,C是圆周上一点(异于A、B),过C作圆O的切线

正确答案
见解析
解析
证明:连结

因为


所以
又因为
所以
又因为直线


又

所以
知识点
已知圆M:








(1)求点G的轨迹C的方程;
(2)过点(2,0)作直线l,与曲线C交于A,B两点,O是坐标原点,设
正确答案
见解析。
解析
(1)


∴|GN|+|GM|=|MP|=6,故G点的轨迹是以M、N为焦点的椭圆,其长半轴长


(2)因为
若存在l使得|

若l的斜率不存在,直线l的方程为x=2,由

故l的斜率存在,设l的方程为


把①、②代入

知识点
已知圆C的极坐标方程为ρ=4cos(θ﹣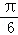
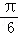
正确答案
见解析
解析
圆C的直角坐标方程为(x﹣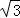
点M的直角坐标为(3
当直线l的斜率不存在时,不合题意;
当直线的斜率存在时,设直线l的方程为;y﹣3=k(x﹣3
圆心到直线的距离为r=2,
因为圆心到直线l的距离 d=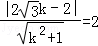
所以k=0或k=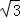
故所求直线的方程为y=3或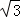
其极坐标方程为ρsinθ=3或ρsin(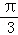
知识点
在平面直角坐标系xOy中,圆的参数方程为
(1)圆的直角坐标方程;
(2)圆的极坐标方程。
正确答案
见解析。
解析
(1)由

①2+②2得:(x﹣2)2+y2=4。
∴圆的直角坐标方程为(x﹣2)2+y2=4;
(2)把
得(ρcosθ﹣2)2+(ρsinθ)2=4,
整理得,ρ2﹣4ρcosθ=0,
∴ρ=0(舍)或ρ=4cosθ。
∴圆的极坐标方程为ρ=4cosθ。
知识点
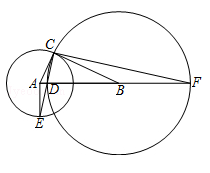
几何证明选讲:如图,已知圆A,圆B都经过点C,BC是圆A的切线,圆B交AB于点D,连结CD并延长交圆A于点E,连结AE,求证DE•DC=2AD•DB。
正确答案
见解析
解析
证明:
∵BC是⊙A的切线,∴AC⊥BC,
∵∠ACD+∠BCD=90°,AC=AE,BC=BD,
∴∠ACD=∠E,∠BCD=∠BDC,
∵∠ADE=∠BDC,∴∠E+∠ADE=90°,
∴AE⊥AB。
延长DB交⊙B于点F,连接FC,则DF=2DB,∠DCF=90°,
∴∠ACD=∠F,∴∠E=∠F,∴Rt△ADE∽Rt△CDF,
∴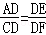
∵DF=2DB,
∴DE•DC=2AD•DB。
知识点
在极坐标系中,圆C: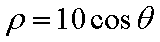
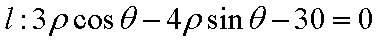
正确答案
见解析
解析
分别将圆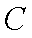
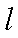
圆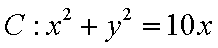

直线
因为圆心
所以
知识点
如图,动点






(1)求轨迹
(2)设直线






正确答案
(1)
解析
解析:(1)设M的坐标为(x,y),显然有x>0,
当∠MBA=90°时,点M的坐标为(2, ±3)
当∠MBA≠90°时;x≠2.由∠MBA=2∠MAB,
有tan∠MBA=
化简得:
综上可知,轨迹C的方程为
(2)由方程

由题意,方程(*)有两根且均在(1,+
所以
解得,m>1,且m
设Q、R的坐标分别为

所以
由m>1,且m
所以

知识点
扫码查看完整答案与解析